The Concept of a Riemann Surface

Hermann Weyl, Gerald R. MacLane

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486470047
• eBook ISBN: 9780486131672
• Topic: Mathematics
• Subtopic: Functional Analysis
• Index: Mathematics

This classic on the general history of functions was written by one of the twentieth century's best-known mathematicians. Hermann Weyl, who worked with Einstein at Princeton, combined function theory and geometry in this high-level landmark work, forming a new branch of mathematics and the basis of the modern approach to analysis, geometry, and topology.
The author intended this book not only to develop the basic ideas of Riemann's theory of algebraic functions and their integrals but also to examine the related ideas and theorems with an unprecedented degree of rigor. Weyl's two-part treatment begins by defining the concept and topology of Riemann surfaces and concludes with an exploration of functions of Riemann surfaces. His teachings illustrate the role of Riemann surfaces as not only devices for visualizing the values of analytic functions but also as indispensable components of the theory.

I. CONCEPT AND TOPOLOGY OF RIEMANN SURFACES

§ 1. Weierstrass’ concept of an analytic function

Let z be a complex variable and a a fixed complex number. With Weierstrass we say that any power series

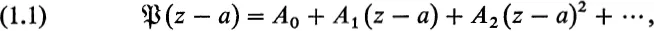
with positive radius of convergence, is a function element with center a. The coefficients A₀, A₁, A₂... are arbitrary complex numbers. The region of convergence of such a power series consists either of the whole z-plane or of a disc |z − a| < r(r > 0), the “convergence disc,” and a subset¹ of the periphery [z − a| = r of that disc.

In its convergence disc (which may be the whole plane regarded as a disc of radius r = ∞), such a function element represents a regular analytic function in the sense of Cauchy. Conversely, it is known from elementary function theory that a uniform regular analytic function may be expanded in a convergent power series (1.1) in any neighborhood |z − a| < r which is contained in the domain of regularity of the function. A power series then serves to represent the function only in a circular part of its domain.

If one starts with a power series which defines the function only in the convergence disc of the series (1.1), then the goal must be to define the function in larger domains of the z-plane without losing the analytic character of the function. The method for this is Weierstrass’ principle of analytic continuation.² It turns out that the plan to conquer a largest possible domain of the z-plane, for the function to be defined, is possible in only one way. But the uniformity (single-valuedness) of the function is usually lost in the process of analytic continuation. This is not to be regarded as a defect; rather it is a great merit that in this fashion also the many-valued analytic functions become amenable to an exact treatment.

If b is a value of z in the convergence disc |z − a| < r, then, as one kno...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Preface
• Contents
• I.  Concept and Topology of Riemann Surfaces
• II.  Functions on Riemann Surfaces
• Index