Equilibrium Statistical Mechanics

E. Atlee Jackson

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486411859
• eBook ISBN: 9780486149394
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

Ideal as an elementary introduction to equilibrium statistical mechanics, this volume covers both classical and quantum methodology for open and closed systems. Introductory chapters familiarize readers with probability and microscopic models of systems, while additional chapters describe the general derivation of the fundamental statistical mechanics relationships. The final chapter contains 16 sections, each dealing with a different application, ordered according to complexity, from classical through degenerate quantum statistical mechanics. Key features include an elementary introduction to probability, distribution, functions, and uncertainty prior to a discussion of statistical mechanics; a review of the concept and significance of energy, together with a discussion of various models of physical systems. A series of appendixes contains helpful information on Gaussian integrals, the error function, the entropy constant, solutions to problems, and other subjects.
A background in integral calculus is assumed, but because material is presented at a reasonable level of complexity, even readers not familiar with quantum mechanics can make use of at least two-thirds of this book. Index. 5 Appendixes. Problems at ends of chapters. Over 100 text figures.

1

Probability

1. FREQUENCY AND PROBABILITY

It is a common experience that the outcome may not always be the same when an experiment is performed a number of times, even though the conditions of the experiment are kept as similar as possible. The reason is that some of the factors that contribute to the outcome of the experiment are not (or cannot) be completely controlled. Simple examples are the “experiments” of rolling dice, drawing cards, tossing coins, or any of the so-called games of chance. Presumably other experiments are nearer to the hearts of physical scientists, but these examples will suffice for the present. In any case, the typical feature of all experiments is that at the end of the experiment one observes some result of interest. To be concise, we shall call those distinct (or mutually exclusive) results of an experiment that are of interest simple events. Therefore the result of each experiment is always one, and only one, simple event. For simplicity we may label these simple events (or simply “events”) with some index i. Thus the two possible events when tossing a coin are heads or tails (i = h, t), whereas there are six possible events when a single die is rolled (i = 1, 2, 3, ..., 6), and so on.

Now if a particular experiment is performed a number of times, say N times, a particular event i may be found to occur n_i times. This fact is of considerable interest, because if the experiment is repeated at a later time, we expect the event i to occur with roughly the same frequency. To investigate this idea we consider the ratio

(1)

This ratio is the fraction of the N experiments that resulted in the event i and is commonly called the frequency of the event i. Although it is useful to know the value of F_i found in some previous group of N experiments, it is important to realize that, if these N experiments are repeated, one cannot expect that the event i will occur the same number of times (n_i). Instead it may occur m_i times. This means that F_i will in general be different for different groups of experiments. Thus, for example, if a coin is tossed twenty times (N = 20), the event “heads” may occur eight times (n_h = 8), so that F_h = 0.4 for that sequence of tosses. If we tossed the coin again twenty times, we would consider it unlikely that heads would turn up again eight times, so we would expect a different value for F _h. Moreover, if the coin were tossed 100 times, the coin might turn up heads 54 times, in which case F_h = 0.54 for that sequence of tosses. If N = 1,000, we might observe n_h = 510, in which case F_h = 0.51. Clearly the frequency of an event depends on the group of experiments being considered.

Since the frequency of an event varies from one group of experiments to another, it is desirable to obtain a quantity that does not depend on any particular group and that at the same time indicates the frequency we can expect in any particular group of experiments. To obtain such a quantity we could, at least in principle, examine the values of the frequency as N becomes extremely large. In the above examples we had

F_h(N = 20) = 0.4, F_h(N = 100) = 0.54, F_h(N = 1,000) = 0.51

As N becomes larger and larger we expect that, if the coin is evenly balanced, the frequency F_h will approach the value 0.50. However, regardless of what the limiting value of the frequency may be when N becomes extremely large, we call this limiting value the probability of a heads (for that coi...

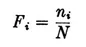
Table of contents

• Title Page
• Copyright Page
• Dedication
• Preface
• Table of Contents
• Introduction
• 1 - Probability
• 2 - Energy
• 3 - Statistical Mechanics
• 4 - Applications of Statistical Mechanics
• Appendices
• INDEX
• Physical Constants and Conversion Factors