Applications of Tensor Analysis

A. J. McConnell

• Publisher: Dover Publications
• Year: 2014
• eBook ISBN: 9780486145020
• Topic: Mathematics
• Subtopic: Vector Analysis
• Index: Mathematics

This standard work applies tensorial methods to subjects within the realm of advanced college mathematics. In its four main divisions, it explains the fundamental ideas and the notation of tensor theory; covers the geometrical treatment of tensor algebra; introduces the theory of the differentiation of tensors; and applies mathematics to dynamics, electricity, elasticity, and hydrodynamics.
Partial contents: algebraic preliminaries (notation, definitions, determinants, tensor analysis); algebraic geometry (rectilinear coordinates, the plane, the straight line, the quadric cone and the conic, systems of cones and conics, central quadrics, the general quadric, affine transformations); differential geometry (curvilinear coordinates, covariant differentiation, curves in a space, intrinsic geometry of a surface, fundamental formulae of a surface, curves on a surface); applied mathematics (dynamics of a particles, dynamics of rigid bodies, electricity and magnetism, mechanics of continuous media, special theory of relativity).

PART I

Algebraic Preliminaries

CHAPTER I

NOTATION AND DEFINITIONS

1. The indicial notation.

The notation of the absolute differential calculus or, as it is frequently called, the tensor calculus, is so much an integral part of the calculus that once the student has become accustomed to its peculiarities he will have gone a long way towards solving the difficulties of the theory itself. We shall therefore devote the present chapter to a discussion of the notation alone, applying it briefly to the theory of determinants, and we shall postpone to the next chapter the tensor theory proper.

If we are given a set of three independent variables, they may be denoted by three different letters, such as x, y, z, but we shall find it more convenient to denote the variables by the same letter, distinguishing them by means of indices. Thus we may write the three variables x₁, x₂, x₃, or, as they may be more compactly written,

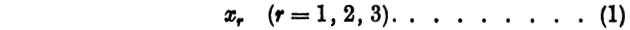
Now in (1) we have written the index r as a subscript, but we could equally well have used superscripts instead, so that the variables would be written x¹, x², x³, or

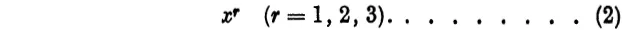
Here it must be understood that x^r does not mean that x is raised to the r^th power, but r is used merely to distinguish the three variables. In the sequel we shall have occasion to use both subscripts and superscripts, and in the next chapter we shall give a special significance to the position of the index. In fact we shall find that, in accordance with the convention adopted later, the form (2) is the appropriate one for our variables and not (1).

A homogeneous linear function of the variables is obviously of the form

where a₁, a₂, a₃ are constants. Thus the coefficients of a linear form can be written

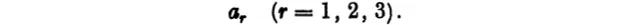
Systems of quantities, which, like x^r and a_r, depend on one index only, are called systems of the first order or simple systems, and the separate terms, x¹, x², x³ and a₁, a₂, a₃ are called the elements or components of the system. It is obvious that a system of the first order has three components. More...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Part I—Algebraic Preliminaries
• Part II.—Algebraic Geometry
• Part. III.—Differential Geometry
• Part IV.—Applied Mathematics
• Appendix. Orthogonal Curvilinear Coordinates in Mathematical Physics
• Bibliography
• Index