Catastrophe Theory and Its Applications

Tim Poston, Ian Stewart

• Publisher: Dover Publications
• Year: 2014
• ISBN:
  9780486143781
• Topic: Matemáticas
• Subtopic: Probabilidad y estadística

This first integrated treatment of the main ideas behind René Thom's theory of catastrophes aims to make them accessible to scientists wishing to apply the theory in their own fields of research. The mathematical basis of the theory is therefore explained with a minimum of technicalities, although some knowledge of the calculus of variables is assumed.
Thom's now-famous list of seven elementary catastrophes, broadly classifying various types of discontinuous change, is elucidated, as are the reasons for its appearance. Nearly half the book concentrates on detailed applications of the theory, emphasizing its uses in the physical sciences where applications can be made quantitative and can be experimentally verified. The more controversial and speculative applications to areas in the social sciences are also mentioned, but not discussed in detail.
Over 200 illustrations help clarify the ideas and applications in this volume, which will be of interest to researchers and postgraduate students in such diverse disciplines as engineering, mathematics, physics, and biology. 1978 edition. Bibliography.

1 Smooth and Sudden Changes

Classical physics (from Newton to General Relativity) is essentially the theory of various kinds of smooth behaviour; above all the awe-inspiring fall of the planets around the sun: unresting, unhasting and utterly regular. Even the wobbles that have dethroned Earth’s rotation as the standard clock happen smoothly. No coherent and mathematical description of celestial mechanics can allow, say, a huge comet falling into the solar system, parting the Red Sea as it passes Earth, and then losing most of its kinetic energy and settling down into an almost perfectly circular orbit as the planet Venus (a widely held pseudoscientific theory). Planets interact much too evenly for that.

1 Catastrophes

Other things, however, jump. Water suddenly boils. Ice melts. Earths and moons quake. Buildings fall. The back of a camel is stable, we are told, under a load of N straws, but breaks suddenly under a load of N+l. Stock markets collapse.

These are sudden changes caused by smooth alterations in the situation: an analogous astronomical event would be the Sun’s steady motion around the galaxy causing the Earth to switch (instantly or in a matter of days) to an orbit ten million miles wider, when some critical position was reached. Such changes are far more awkward for prediction and analysis than the stars in their courses, and the sciences (from physics to economics) are still gathering together the analytical techniques to handle such jumping behaviour.

Now there are many kinds of jump phenomena. There are forces that build up until friction can no longer hold them: the roar of an earthquake, and the rustle of rhubarb growing, are made by the movements when friction gives way. There is a critical population density below which certain creatures grow up as grasshoppers, above which as locusts: this is why locusts, when they do occur, do so in a huge swarm. A cell suddenly changes its reproductive rhythm and doubles and redoubles, cancerously. A man has a vision on the road to Tarsus.

Many of these still defy analysis: many have been analysed, with a tremendous variety of mathematical methods. We shall be concerned in this book with one particular mathematical context which covers a broad range of such phenomena in a coherent manner. The techniques involved were developed by the French mathematician René Thom and became widely known through his book Stabilité Structurelle et Morphogénèse [1] in which he proposed them as a foundation for biology. The sudden changes involved were christened by Thom catastrophes, to convey the feeling of abrupt or dramatic change: the word’s overtones of disaster are, for most applications, misleading. The subject has since become known as catastrophe theory, a phrase which is open to a variety of interpretations depending on the scope accorded it.

These techniques apply most directly (but far from exclusively) to systems that through varying situations seek at each moment to minimize some function (e.g. energy) or maximize one (e.g. entropy). We shall clarify in Chapter 3 what this means mathematically. For the present a good picture is that of a ball rolling around a landscape and ‘seeking’ through the agency of gravitation to settle in some position which, if not the lowest possible, is at least lower than any other nearby. (But meanwhile the landscape itself is changing.) The particular geometrical forms that arise in this setting have become known, following Thom, as elementary catastrophes, in the sense of fundamental entities (like chemical elements) and their use as expounded in this book is thus ‘elementary catastrophe theory’ (a phrase misinterpreted by Sussman and Zahler [la] to resemble' ‘elementary arithmetic’), though it is deep both mathematically and scientifically. For some systems more complicated phenomena can occur (we give an easily explained example in Chapter 17 Section 7), whose onset Thom [1] classes collectively as generalized catastrophes. Their theory is by no means so complete.

Physical intuition is important for the understanding of catastrophe theory. In this chapter we shall describe three simple physical systems exhibiting typical catastrophic behaviour, having the advantage that (unlike earthquakes or stock markets) they are simple enough to build, and small enough to carry around. In addition they may be used for elementary experiments. They are well adapted to analysis, although we shall not analyse them at this stage, and will be used repeatedly as examples. The reader will find his intuition very much assisted if he actually makes them (for which reason we give some practical indications as to their construction) and plays with them. No description can compete with direct experience. But it must be emphasized that these machines bear a similar relation to catastrophe theory as do the toys known as ‘Newton’s cradle’ and ‘the simple pendulum’ to Newtonian mechanics.

2 The Zeeman Catastrophe Machine

We begin with the first machine invented. E. C. Zeeman, of the University of Warwick, devised it in 1969: after three weeks of experimentation with rubber bands and paperclips he refined it to the version we describe. The first appearance in print was Zeeman [2]: other references include Poston and Woodcock [3] and Dubois and Dufour [4].

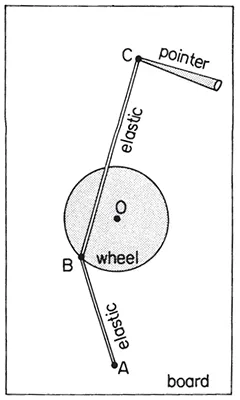
Fig. 1.1

It consists of a wheel (Fig. 1.1) mounted flat against a board, able to turn freely, and not too heavy: too much friction resisting the movement or inertia prolonging it obscure the behaviour we wish to study. To one point (B) on its edge are attached two lengths of elastic. One of these has its other end fixed to the board at point (A), far enough from the hub (O) of the wheel to keep the elastic BA always tight. The second has its other end (C) attached to a pointer, to be held in the hand. (The position of C can thus be controlled from a little distance without obscuring it.) Dimensions which work well in practice are a wheel of radius 3 cm, OA of length 12 cm, and each piece of elastic of unstretched length 6 cm.

Regardless of the radius r of the wheel, the unstretched lengths a and b of the elastic BA and BC, and the distance OA (as long as this is more than a + r) the machine will show qualitatively the behaviour to be described below. This is a part of the property of ‘structural stability’ which we discuss later: changes in the parameters make no essential qualitative difference, in a sense to be made precise at the relevant time. However, we shall be analysing the machine for one particular set of numbers, with the aid of computer graphics; so we now give detailed instructions for a machine whose behaviour has exactly the geometry drawn by the computer.

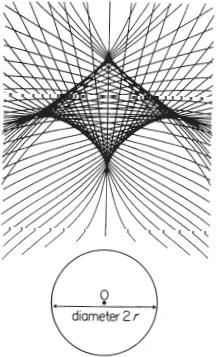
Fig. 1.2

Photocopy Fig. 1.2. An enlarged or reduced photograph is perfectly acceptable, since scale does not affect the behaviour, or its subsequent analysis. Mount the result on board or heavy card, and attach a wheel at point O. Attach a stiff wire to the wheel, perpendicular to the plane of the board, at radius r from O. (It may be convenient to make the wheel itself a little larger, since only the position of the wire matters, and combine the mounting of the wire with that of the wheel as in Fig. 1.3.) Fix another stiff wire perpendicular to the board at A. File a groove round each wire, both at the same distance above the board, and higher than any central raised point of the wheel. Take a piece of good quality rubber cord (not a cut rubber band or sewing elastic: better the square section cord sold for catapults† or model aeroplanes), some-what longer than four times the diameter 2r shown for the wheel in your copy of Fig. 1.2. Attach the middle to the wire at A, binding it with cotton to form a loop round the groove (Fig. 1.4(a)). Mark the point whose distance along the unstretched elastic is 2r, holding the elastic doubled and st...