Probabilistic Metric Spaces

B. Schweizer, A. Sklar, A. Sklar

• Publisher: Dover Publications
• Year: 2011
• eBook ISBN: 9780486143750
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This distinctly nonclassical treatment focuses on developing aspects that differ from the theory of ordinary metric spaces, working directly with probability distribution functions rather than random variables. The two-part treatment begins with an overview that discusses the theory's historical evolution, followed by a development of related mathematical machinery. The presentation defines all needed concepts, states all necessary results, and provides relevant proofs.
The second part opens with definitions of probabilistic metric spaces and proceeds to examinations of special classes of probabilistic metric spaces, topologies, and several related structures, such as probabilistic normed and inner-product spaces. Throughout, the authors focus on developing aspects that differ from the theory of ordinary metric spaces, rather than simply transferring known metric space results to a more general setting.

1

Introduction and Historical Survey

1.0. Introduction

The 19th century, which marks the beginning of the modern age of science, was an era of great advances in the art of measurement. These advances stimulated a corresponding concern with the accompanying errors. Until the early part of this century, however, it was still believed that through careful design and ample data the error in any measurement could be made arbitrarily small. The advent of quantum mechanics shattered this belief, for here the uncertainties of the measurements are inherent in the measurement process itself and in principle cannot be removed.

Today, in the fourth quarter of the 20th century, the existence of such inherent uncertainties and thresholds is a generally accepted fact. This is true not only in physics but also in areas such as psychometrics [S. Stevens 1959], communication theory [Shannon 1948; Brillouin 1956], and pattern recognition [Duda and Hart 1973; Yakimovsky 1976; Prager 1979]. It is also central to various mathematical disciplines, such as cluster analysis [Janowitz 1978; Shepard 1980] and interval analysis [Moore 1979]. However, in virtually all the mathematical models built to describe these various situations it is assumed that the measurements in question are made with respect to a rigid reference frame. Remarks to the effect that this assumption may be unsatisfactory and that some of the uncertainties should be built into the geometry are scattered here and there in the literature [Poincaré 1905, 1913; Hjelmslev 1923; de Broglie 1935; Black 1937; Weyl 1952; Bom 1955; Oppenheimer 1962], along with suggestions on the proper way of doing this [Penrose and MacCullum 1973; Penrose 1975]. There are also some serious attempts in this direction [Eddington 1953; Rosen 1947, 1962; Blokhintsev 1971, 1973; Frenkel 1977]. This book is a direct outgrowth of one of these attempts, namely, the theory of probabilistic metric spaces as initiated by K. Menger in 1942.

1.1. Beginnings

The first abstract formulation of the notion of distance is due to M. Fréchet [1906]. This notion, which was later given the name “metric space” (“metrischer Raum”) by F. Hausdorff [1914], is based on the introduction of a function d that assigns a nonnegative real number d(p, q) (the distance between p and q) to every pair (p, q) of elements (points) of a nonempty set S. This function is assumed to satisfy the following conditions:

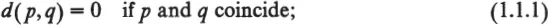
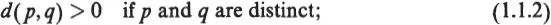
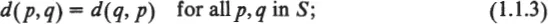
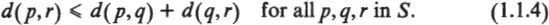
Condition (1.1.4), whose antecedents go back at least to Euclid’s Proposition I.20, is the triangle inequality.

Any function d satisfying (1.1.1)–(1.1.4) is a metric on S. (Occasionally it is convenient to drop (1.1.2), in which case d is a pseudometric on S.) A metric space is a pair (S, d) where S is a set and d is a metric on S.

In 1942 K. Menger, who had played a major role in the development of the theory of metric spaces (see [Menger 1928, 1930, 1932, 1954]), proposed a probabilistic generalization of this theory. Specifically, he proposed replacing the number d(p, q) by a real function F_pq whose value F_pq(x), for any real number x, is interpreted as the probability that the distance between p and q is less than x. Since probabilities can neither be negative nor be greater than 1, we have

for every real x, and clearly we also have

whenever x < y. Hence F_pq is a probability distribution function.

Other conditions on the functions F_pq are also immediate. Thus, since distances cannot be negative, we have

Similarly, (1.1.1), (1.1.2), and (1.1.3) yield the following:

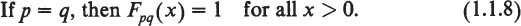
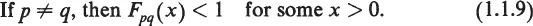
In contradistinction, the probabilistic generalization of the triangle inequality (1.1.4) is quite another matter. Even at the outset Menger and A. Wald proposed different generalizations, and the study of alternative triangle inequalities has been a central theme in the development of the theory of probabilistic metric spaces. The major steps in this development are traced in the next few sections.

1.2. Menger, 1942

In his original paper, Menger [1942] defined a statistical metric space¹ as a set S together with an associated family of probability distribution functi...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Preface to the Dover Edition
• Preface
• Special Symbols
• Chapter 1. Introduction and Historical Survey
• Chapter 2. Preliminaries
• Chapter 3. Metric and Topological Structures
• Chapter 4. Distribution Functions
• Chapter 5. Associativity
• Chapter 6. Copulas
• Chapter 7. Triangle Functions
• Chapter 8. Probabilistic Metric Spaces
• Chapter 9. Random Metric Spaces
• Chapter 10. Distribution-Generated Spaces
• Chapter 11. Transformation-Generated Spaces
• Chapter 12. The Strong Topology
• Chapter 13. Profile Functions
• Chapter 14. Betweenness
• Chapter 15. Supplements
• References
• Index
• Errata
• Notes
• Supplementary References