Spherical Models

Magnus J. Wenninger

• Publisher: Dover Publications
• Year: 2014
• eBook ISBN: 9780486143651
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

Well known through the work of Buckminster Fuller, models of spherical polyhedral excite the imaginations not only of mathematicians, architects and engineers but also of artists and designers. This book, concerned with polyhedrons, sphere tilings, and dome structures, offers a well-illustrated, practical approach to creating a host of beautiful and interesting models, including starfaced spherical forms that can serve as basic structures for geodesic domes.
Employing only the most elementary mathematical principles, the text initially provides complete instructions for making spherical models from five regular solids, using only circular bands of paper, a ruler and a compass. Also discussed is tessellation, or tiling, on a sphere and how to make spherical models of all the semiregular solids. The volume concludes with a discussion of the relationship of polyhedral to geodesic domes and directions for building models of the domes.
Abundantly illustrated with photographs, drawings, and computer graphics of attractive geometrical models, this volume will appeal to a wide range of readers—from students and teachers of mathematics, art, design, architecture and engineering, to recreational mathematics enthusiasts and builders of geodesic domes.

IV. Geodesic domes

If you have ever had the opportunity of looking closely at a geodesic dome, your first impression may well have been that all its triangles are equilateral. A second impression may well have been that these triangles seem to group themselves into hexagons, six around a point. Closer inspection may have revealed to you that some groups are not hexagons but rather pentagons. So obviously these triangles at least cannot be equilateral.

It is now time to enter more deeply into a study of geodesic domes. What you have done so far in making models of spherical polyhedrons will serve as a good background for this investigation.

Plate 31.A 4-frequency icosahedral geodesic dome.{3,5+}_4,0

Photo 33. Dodecahedron (omitting a) or pentakisdodecahedron. {3, 5+}_1,1

Moreover the procedure for making spherical models, as it has been developed in this book, can easily be extended to making models of geodesic domes in paper. For this purpose it is good to return to the regular and semiregular models because some variations here will provide an easy introduction to this topic.

The simplest geodesic domes

Since there are three regular spherical models, the tetrahedral, octahedral, and icosahedral, you may already have made the variations of these that eliminated a and r. The tetrahedron made in this way has four equilateral triangles, the octahedron has eight, and the icosahedron has twenty. These are in fact the simplest examples of geodesic domes. They do not look very much like geodesic domes as generally known however. The spherical dodecahedron will be the first one to take on such an appearance, provided you make it retaining r and eliminating only a. This polyhedron is more correctly called a pentakisdodecahedron. The name denotes the number of its faces: 5 x 12 = 60. Here each face of the dodecahedron has been decomposed into a set of five isosceles triangles. Use the circular band shown in Fig. 40 to make this model; see also Photo 33.

Once the model is made examine it and you will see that it has triangles that your eye can arrange into groups of six or into groups of five. The incenters of these groups are called hexavalent and pentavalent vertices. This is an important feature of geodesic domes as generally known. You will find references to this feature again and again in what follows. The pentakisdodecahedron model has twelve pentavalent vertices and twenty hexavalent ones.

The icosidodecahedron becomes an example of a geodesic dome if all its triangles are allowed to remain as equilateral and the pentagons are changed into groups of five isosceles triangles each. See Fig. 41 for the layout of the bands. Photo 34 shows the complete model. This model has twelve pentavalent vertices and thirty hexavalent ones. Notice too that as the number of elements increases the models become more attractive.

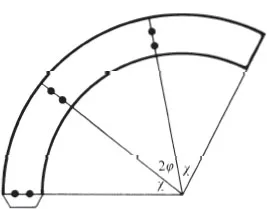
Fig.40.Band for a sperical dodecahedron(omitting a)or for a pentakisdodecahedron

The truncated icosahedron has twelve pentagon faces and twenty hexagon faces. If the pentagons are constructed with five elements each and the hexagons with six elements each, another model of a genuine geodesic dome results. See Fig. 42 for the layout of the bands and Photo 35 for the complete model. This model has twelve pentavalent vertices and eighty hexavalent ones. Not only has the number of elements grown larger here, but the number of hexavalent vertices as well. Notice that the number of pentavalent vertices remains constant at twelve. If you find it difficult to verify the count of hexavalent vertices in this case, do not worry about it now. Later on a formula will b...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Foreword
• Preface
• Introduction
• Chapter1 I.The regular spherical models
• Chapter2 II.The semiregular spherical models
• Chapter3 III.Variations
• Chapter4 IV.Geodesic domes
• Chapter5 V.Miscellaneous models
• Epilogue
• Appendix
• References
• Index