Fundamentals of Number Theory

William J. LeVeque

• Publisher: Dover Publications
• Year: 2014
• ISBN:
  9780486141503
• Topic: Mathematics
• Subtopic: Number Theory
• Index: Mathematics

This excellent textbook introduces the basics of number theory, incorporating the language of abstract algebra. A knowledge of such algebraic concepts as group, ring, field, and domain is not assumed, however; all terms are defined and examples are given — making the book self-contained in this respect.
The author begins with an introductory chapter on number theory and its early history. Subsequent chapters deal with unique factorization and the GCD, quadratic residues, number-theoretic functions and the distribution of primes, sums of squares, quadratic equations and quadratic fields, diophantine approximation, and more. Included are discussions of topics not always found in introductory texts: factorization and primality of large integers, p-adic numbers, algebraic number fields, Brun's theorem on twin primes, and the transcendence of e, to mention a few.
Readers will find a substantial number of well-chosen problems, along with many notes and bibliographical references selected for readability and relevance. Five helpful appendixes — containing such study aids as a factor table, computer-plotted graphs, a table of indices, the Greek alphabet, and a list of symbols — and a bibliography round out this well-written text, which is directed toward undergraduate majors and beginning graduate students in mathematics. No post-calculus prerequisite is assumed. 1977 edition.

1

Introduction

1.1 WHAT IS NUMBER THEORY?

This could serve as a first attempt at a definition: it is the study of the set of integers 0, ±1, ±2, . . . , or some of its subsets or extensions, proceeding on the assumption that integers are interesting objects in and of themselves, and disregarding their utilitarian role in measuring. This definition might seem to include elementary arithmetic, and in fact it does, except that the concern now is to be with more advanced and more subtle aspects of the subject. A quick review of elementary properties of the integers is incorporated with some other material, which may or may not be new to the reader, in Sections 1.2 and 1.3.

To get some idea of what the subject comprises, let us go back to the seventeenth century, when the modern epoch opened with the work of Pierre de Fermat [fairmati]. One of Fermat’s most beautiful theorems is that every positive integer can be represented as the sum of the squares of four integers, for example,

He announced this theorem in 1636, but the first published proof of it was given by Joseph-Louis Lagrange in 1770. It could serve as the ideal example of a theorem in number theory: it is elegant and immediately comprehensible; it reveals a subtle and unexpected relationship among the integers; it is the best theorem of its kind (7 cannot be represented with fewer than four squares); and it says something about an infinite class of integers. The last is an important qualification, as it distinguishes between theorems and numerical facts. It is a fact, and perhaps even an interesting one, that 1729 is the smallest positive integer having two distinct representations as the sum of two cubes (10³ + 9³ and 12³ + 1³), but this would hardly be called a theorem since it can be verified by examining the finite set 1, 2, 3, . . . , 1729. On the other hand, the assertion that there are only finitely many integers having two or more such representations is deceptive; it seems to say something about a finite set, but in fact it cannot be proved by examining any specific finite set, nor can it be disproved in this way. Thus it would be a significant theorem if it were true. (It is not; that, too, is a significant theorem.)

Pierre de Fermat (1601–65)

Fermat was a lawyer by profession, well versed in ancient languages and steeped in classical culture. There were no scientific journals then, and he was not inclined to write out proofs. Instead, he communicated his results by letter, especially to Father M. Mersenne, who maintained an enormous correspondence throughout Europe. Fermat anticipated Descartes in analytic geometry and Newton and Leibniz in differential calculus, but his work was not well known because he failed to publish his books on these subjects. His fame rests chiefly on his work in number theory, where he was without peer. The groundwork that had been laid for him by the Greeks and others is discussed in the final section of this chapter.

An even more famous assertion credited to Fermat is what is sometimes called his Last Theorem, which says that if n is an integer larger than 2, then the equation xⁿ + yⁿ = zⁿ has no solution in positive integers x, y, z. Fermat claimed to have proved this, but as was his habit he did not reveal the proof. This seems to be the only recorded instance in which he claimed a result that has never been verified (although he did announce an erroneous conjecture, discussed below). Lacking a proof, mathematicians today tend to call it the Fermat Problem, rather than Theorem; it is the oldest, and possibly the most famous, unsolved problem in mathematics. A single counterexample would suffice to destroy it, of course, but finding such a quadruple x, y, z, n, if there is one, might well be beyond the capacity of present or future computers, since the equation is now known to have no solution for n < 100,000, and in any case to have only solutions with one of x, y, or z larger than n²ⁿ. (The known universe would accommodate only about 10¹²³ proton-sized objects, close-packed.)

One of the basic concepts in number theory is that of a prime number. An integer p is prime if p ≠ ±1 and the equation p = ab has no solution in integers a and b except those for which a = ±1 or ...

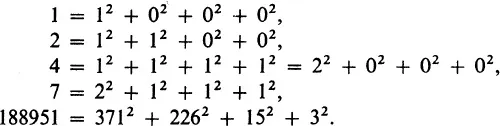
Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• Chapter 1 Introduction
• Chapter 2 Unique Factorization and the GCD
• Chapter 3 Congruences and the Ring Zm
• Chapter 4 Primitive Roots and the Group Um
• Chapter 5 Quadratic Residues
• Chapter 6 Number-Theoretic Functions and the Distribution of Primes
• Chapter 7 Sums of Squares
• Chapter 8 Quadratic Equations and Quadratic Fields
• Chapter 9 Diophantine Approximation
• Bibliography
• Appendix
• Index