Information Theory

Robert B. Ash

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486665214
• eBook ISBN: 9780486141459
• Topic: Technology & Engineering
• Subtopic: Probability & Statistics
• Index: Technology & Engineering

Developed by Claude Shannon and Norbert Wiener in the late 1940s, information theory, or statistical communication theory, deals with the theoretical underpinnings of a wide range of communication devices: radio, television, radar, computers, telegraphy, and more. This book is an excellent introduction to the mathematics underlying the theory.
Designed for upper-level undergraduates and first-year graduate students, the book treats three major areas: analysis of channel models and proof of coding theorems (chapters 3, 7, and 8); study of specific coding systems (chapters 2, 4, and 5); and study of statistical properties of information sources (chapter 6). Among the topics covered are noiseless coding, the discrete memoryless channel, effort correcting codes, information sources, channels with memory, and continuous channels.
The author has tried to keep the prerequisites to a minimum. However, students should have a knowledge of basic probability theory. Some measure and Hilbert space theory is helpful as well for the last two sections of chapter 8, which treat time-continuous channels. An appendix summarizes the Hilbert space background and the results from the theory of stochastic processes necessary for these sections. The appendix is not self-contained but will serve to pinpoint some of the specific equipment needed for the analysis of time-continuous channels.
In addition to historic notes at the end of each chapter indicating the origin of some of the results, the author has also included 60 problems with detailed solutions, making the book especially valuable for independent study.

CHAPTER ONE

A Measure of Information

1.1. Introduction

Information theory is concerned with the analysis of an entity called a “communication system,” which has traditionally been represented by the block diagram shown in Fig. 1.1.1. The source of messages is the person or machine that produces the information to be communicated. The encoder associates with each message an “object” which is suitable for transmission over the channel. The “object” could be a sequence of binary digits, as in digital computer applications, or a continuous waveform, as in radio communication. The channel is the medium over which the coded message is transmitted. The decoder operates on the output of the channel and attempts to extract the original message for delivery to the destination. In general, this cannot be done with complete reliability because of the effect of “noise,” which is a general term for anything which tends to produce errors in transmission.

Information theory is an attempt to construct a mathematical model for each of the blocks of Fig. 1.1.1. We shall not arrive at design formulas for a communication system; nevertheless, we shall go into considerable detail concerning the theory of the encoding and decoding operations.

It is possible to make a case for the statement that information theory is essentially the study of one theorem, the so-called “fundamental theorem of information theory,” which states that “it is possible to transmit information through a noisy channel at any rate less than channel capacity with an arbitrarily small probability of error.” The meaning of the various terms “information,” “channel,” “noisy,” “rate,” and “capacity” will be clarified in later chapters. At this point, we shall only try to give an intuitive idea of the content of the fundamental theorem. Imagine a “source of information” that produces a sequence of binary digits (zeros or ones) at the rate of 1 digit per second. Suppose that the digits 0 and 1 are equally likely to occur and that the digits are produced independently, so that the distribution of a given digit is unaffected by all previous digits. Suppose that the digits are to be communicated directly over a “channel.” The nature of the channel is unimportant at this moment, except that we specify that the probability that a particular digit is received in error is (say) 1/4, and that the channel acts on successive inputs independently. We also assume that digits can be transmitted through the channel at a rate not to exceed 1 digit per second. The pertinent information is summarized in Fig. 1.1.2.

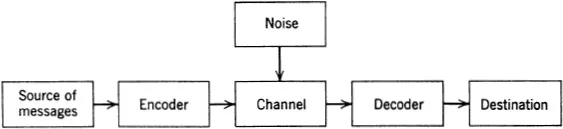
Fig. 1.1.1. Communication system.

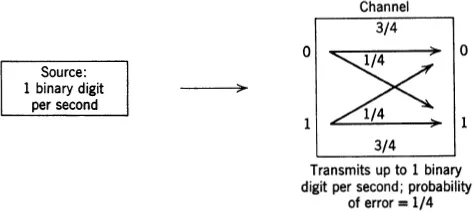
Fig. 1.1.2. Example.

Now a probability of error of 1/4 may be far too high in a given application, and we would naturally look for ways of improving reliability. One way that might come to mind involves sending the source digit through the channel more than once. For example, if the source...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• Chapter One: A Measure of Information
• Chapter Two: Noiseless Coding
• Chapter Three: The Discrete Memoryless Channel
• Chapter Four: Error Correcting Codes
• Chapter Five: Further Theory of Error Correcting Codes
• Chapter Six: Information Sources
• Chapter Seven: Channels with Memory
• Chapter Eight: Continuous Channels
• Appendix
• Tables of Values of −log2 p and −p log2 p
• Solutions to Problems
• References
• Index