College Geometry

An Introduction to the Modern Geometry of the Triangle and the Circle

Nathan Altshiller-Court

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486458052
• eBook ISBN: 9780486141374
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

Translated into many languages, this book was in continuous use as the standard university-level text for a quarter-century, until it was revised and enlarged by the author in 1952. World-renowned writer and researcher Nathan Altshiller-Court (1881–1968) was a professor of mathematics at the University of Oklahoma for more than thirty years. His revised introduction to modern geometry offers today's students the benefits of his many years of teaching experience.
The first part of the text stresses construction problems, proceeding to surveys of similitude and homothecy, properties of the triangle and the quadrilateral, and harmonic division. Subsequent chapters explore the geometry of the circle—including inverse points, orthogonals, coaxals, and the problem of Apollonius and triangle geometry, focusing on Lemoine and Brocard geometry, isogonal lines, Tucker circles, and the orthopole. Numerous exercises of varying degrees of difficulty appear throughout the text.

III

PROPERTIES OF THE TRIANGLE

A. PRELIMINARIES

54. Problem. Divide a given segment, AB, internally and externally in a given ratio p:q.

Through the ends A, B (Fig. 39) of the given segment draw any pair of-parallel lines AF, GBH, and lay off AF = p, BG = BH = q.

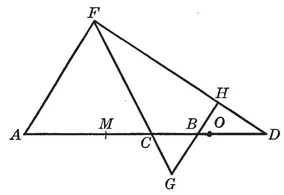
FIG. 39

The lines FG, FH meet the line AB in the required points C, D, as is readily seen from the two pairs of similar triangles CAF and CBG, DAF and DBH.

55. Remark I. To avoid ambiguity the statement of the problem should indicate whether the segments of AB proportional to p and q shall be adjacent to A and B, respectively, as is the case of the figure, or to B and A. Otherwise there is another pair of points, C′, D′, the symmetric of C, D with respect to the midpoint M of AB, which solves the problem. However, in actual applications the nature of the problem usually distinguishes between the points A, B and thus leads to only one pair of points of division.

56. Remark II. If p > q, we have AC > CB and AD > DB, so that the midpoint M of AB lies outside the segment CD. The same relative position of the points M, C, D prevails, if p < q.

If p = q, the point C coincides with M, and there is no external point of division, since FH is then parallel to AB.

57. Theorem. If the points C, D divide the segment AB internally and externally in the ratio p:q, the points B, A divide the segment DC internally and externally in the ratio (p + q): (p – q).

We have (Fig. 39):

AC:CB = p:q, AD:DB = p:q;

hence:

1. (AC + CB):CB = (p + q):q, (AD – DB):DB = (p – q):q,
2. AC: (AC + CB) = p: (p + q), AD: (AD – DB) = p: (p – q).

Substituting AB for AC + CB and for AD – DB in (1) and (2), and combining the two proportions in each of these two lines we obtain:

DB:BC = (p + q) : (p – q),

DA:AC = (p + q): (p – q).

58. COROLLARY. If AB = a and CD = b, we have b = 2 apq: (p² – q²).

Indeed, we have:

AD:AB = p: (p – q), AC:AB = p:(p + q), CD = AD – AC;

hence the announced result.

59. Definitions. Instead of saying that the points C, D (§ 57) divide the segment AB internally and externally in the same ratio, we shall sometimes say that the points C, D divide the segment AB harmonically, or that the points C, D separate the points A, B harmonically, or that the points C, D are harmonic conjugates with respect to the points A, B.

The preceding proposition (§ 57) states that the relation between the two pairs of points is mutual, so that the points A, B, in turn, divide the segment CD harmonically, and the points A, B separate the points C, D harmonically. We may thus refer to the two pairs of points A, B and C, D as two pairs of harmonic points, and to the two segments AB, CD as two harmonic segments.

60. Problem. Given three collinear points A, B, C, construct the harmonic conjugate D of C with respect to the points A, B.

Through the points A, B draw any pair of parallel lines AF, GBH (Fig. 39) and through C any transversal meeting AF, BG in F, G. On GB lay off BH = BG. The line FH meets AB in the required point D.

61. Theorem. The feet of the two pairs of perpendiculars dropped upon a given line from two pairs of harmonic points are also two pairs of harmonic points.

Indeed, the perpendiculars are four parallel lines; hence the segments determined ...

Table of contents

• Title Page
• Copyright Page
• Dedication
• PREFACE
• ACKNOWLEDGMENTS
• Table of Contents
• TO THE INSTRUCTOR
• TO THE STUDENT
• I - GEOMETRIC CONSTRUCTIONS
• II - SIMILITUDE AND HOMOTHECY
• III - PROPERTIES OF THE TRIANGLE
• IV - THE QUADRILATERAL
• V - THE SIMSON LINE
• VI - TRANSVERSALS
• VII - HARMONIC DIVISION
• VIII - CIRCLES
• IX - INVERSION
• X - RECENT GEOMETRY OF THE TRIANGLE
• HISTORICAL AND BIBLIOGRAPHICAL NOTES
• LIST OF NAMES
• INDEX