The Elements of Dynamic Symmetry

Jay Hambidge

• Publisher: Dover Publications
• Year: 2012
• eBook ISBN: 9780486140254
• Topic: Kunst
• Subtopic: Kunsttechniken

Is design intuitive or is it consciously and methodically worked out? Are there basic rules governing design that, when learned, will facilitate the creative process? These questions have been asked by artists, art historians, and art critics throughout the ages.
Convinced that design was not purely instinctive, Jay Hambidge (1867–1924) spent much of his life searching for the technical bases of design. He found his answer in dynamic symmetry, one of the most provocative and stimulating theories in art history. Hambidge's study of Greek art convinced him that the secret of the beauty of Greek design was in the conscious use of dynamic symmetry — the law of natural design based upon the symmetry of growth in man and in plants. But Hambidge, who was not only a theoretician but also a practicing artist, did much more than analyze classical art and its principles of design: he worked out a series of root rectangles that the artist, using the simple mathematics supplied in this book, can easily follow and apply in his own work.
Originally published as a series of lessons in Hambidge's magazine, The Diagonal, this engrossing book explains all the basic principles of dynamic symmetry. Part I sets forth the fundamental rectangles with their simple divisions based on the proportioning law found in nature; Part II explains compound rectangles, many of which were taken from or suggested by analysis of objects of Greek art.
Whether read for its historical importance in art theory, for its illuminating insights into Greek art, or for its practical value to today's artists and commercial designers, The Elements of Dynamic Symmetry has much to offer anyone who is interested in the principle of design.

PART I

SIMPLE RECTANGLES

LESSON 1

The Square (1 or Unity).

THESE lessons will deal entirely with the fundamental principles of symmetry as they are found in nature and in Greek art; no attempt will be made to show their application to specific examples of nature or of art.

THE BASES OF DYNAMIC SYMMETRY

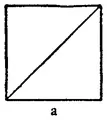
The Square and its diagonal and the square
and the diagonal to its half

The square and its diagonal furnish the series of root rectangles. The square and the diagonal to its half furnish the series of remarkable shapes which constitute the architectural plan of the plant and the human figure.

The most distinctive shape which we derive from the architecture of the plant and the human figure, is a rectangle which has been given the name “root-five.” It is so called because the relationship between the end and side is as one to the square root of five, 1.:2.2360 plus.³

As a length unit the end cannot be divided into the side of a root-five rectangle, because the square root of five is a never-ending fraction. We naturally think of such a relationship as irrational. The Greeks, however, said that such lines were not irrational, because they were commensurable or measurable in square. This is really the great secret of Greek design. In understanding this measurableness of area instead of line the Greek artists had command of an infinity of beautiful shapes which modern artists are unable to use. The relationship between the end and side of a root-five rectangle is a relationship of area and not line, because as lengths one cannot be divided into the other, but the square constructed on the end of a root-five rectangle is exactly one-fifth the area of the square constructed on the side. The areas of rectangles which have this measurable relationship between end and side possess a natural property that enables us to divide them into many smaller shapes which are also measurable parts of the whole.

A simple method for constructing all the root rectangles is shown in Fig. 1.⁴

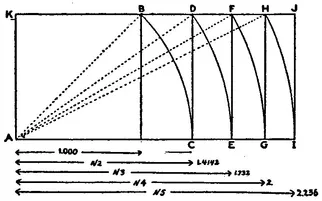
Fig. 1

In Fig. 1, AB is a square whose side is assumed to be unity, or 1. Since the diagonal of a square whose side is unity equals the square root of two, the diagonal AB equals the square root of two. With A as center and AB as radius describe the arc of a circle, BC. The line AC equals AB, or the square root of two. AD is therefore a root-two rectangle. Numerically the line KA equals unity or 1. and the line AC equals the square root of two, or 1.4142.

The diagonal of the root-two rectangle, AD, equals the square root of three. By the same process the line AE is made equal to AD, or the square root of three. AF is therefore a root-three rectangle. Numerically its height, KA, equals unity or 1.; its length, AE, equals the square root of three, or 1.732.

The diagonal of the root-three rectangle, AF, equals the square root of four. By the same process the line AG is made equal to AF or the square root of four. AH is therefore a root-four rectangle. Numerically its height, KA, equals unity or 1.; its length, AG, equals the square root of four, or 2. The root-four rectangle is thus seen to be composed of two squares, since its length equals twice its height.

The diagonal of the root-four rectangle, AH, equals the square root of five. By the same process the line AI is made equal to AH, or the square root of five. AJ is therefore a root-five rectangle. Numerically its height, KA, equals unity or 1.; its length, AI, equals the square root of five, or 2.236.

This process can be carried on to infinity. For practical purposes no rectangles beyond the root-five rectangle need be considered. In Greek art a rectangle higher than root-five is seldom found. When one does appear it is almost invariably a compound area composed of two smaller rectangles added together.

In any of the root rectangles a square on the longer side is an even multiple of a square on the shorter side. Thus a square constructed on the line AC has twice the area of the square on KA; the square on AE has three times the area of the square on KA; the square on AG has four times the area of the square on KA; the square on AI has five times the area of the square on KA. This is demonstrated graphically in the following diagrams, Fig. 2.

The linear proportions 1, √2, √3, √4, √5, etc., are based on the proportions of square areas derived by diagonals from a generating square.⁵

The linear proportions 1, √2, √3, √4, √5, are geometrically established as in Fig. 2.

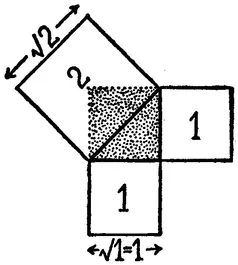
Fig. 2a

In Fig. 2a this unit square is indicated by shading. Its diagonal divides it into two right-angled triangles, one of which is marked by heavy lines. The 47th proposition of the first book of Euclid proves that the square on the hypotenuse of a right-angled triangle equals the sum of the squares on the other two sides. Since the are...

Table of contents

• DOVER BOOKS ON ART INSTRUCTION
• Title Page
• Copyright Page
• Table of Contents
• PREFACE
• Praise
• INTRODUCTION - Synthesis and Analysis.—The Difference between Static and Dynamic Symmetry.—Sources for the Study of Dynamic Symmetry.
• THE ELEMENTS OF DYNAMIC SYMMETRY - THE DYNAMIC SYMMETRY OF THE PLANT
• PART I - SIMPLE RECTANGLES
• PART II - COMPOUND RECTANGLES
• DEFINITIONS
• GLOSSARY
• A CATALOG OF SELECTED DOVER BOOKS IN ALL FIELDS OF INTEREST