Theory of Relativity

W. Pauli

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486319223
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

Wolfgang Pauli (1900–1958) was one of the 20th-century's most influential physicists. He was awarded the 1945 Nobel Prize for physics for the discovery of the exclusion principle (also called the Pauli principle). A brilliant theoretician, he was the first to posit the existence of the neutrino and one of the few early 20th-century physicists to fully understand the enormity of Einstein's theory of relativity.
Pauli's early writings, Theory of Relativity, published when the author was a young man of 21, was originally conceived as a complete review of the whole literature on relativity. Now, given the plethora of literature since that time and the growing complexity of physics and quantum mechanics, such a review is simply no longer possible.
In order to maintain a proper historical perspective of Professor Pauli's significant work, the original text is reprinted in full, in addition to the author's insightful retrospective update of the later developments connected with relativity theory and the controversial questions that it provokes.
Pauli pays special attention to the thorny problem of unified field theories, its connection with the range validity of the classical field concept, and its application to the atomic features of nature. While an early skeptic of solutions along classical lines, Pauli's alternative model was subsequently supported by the newer epistemological analysis of quantum or wave mechanics. Given the many pieces of the puzzle yet to be fitted into a cohesive picture of relativity, the differences of opinion on the relation of relativity theory to quantum theory are merging into one of science's great open problems.
Pauli provides additional informative views on: problems beyond the original frame of special and general relativity; the conflict between "classical physics" and the quantum mechanical approach; the importance of Einsteinian theory in the development of physics; and finally, the epistemological analysis of the finiteness of the quantum of action and the move away from naïve visualizations.

PART I. THE FOUNDATIONS OF THE SPECIAL THEORY OF RELATIVITY

1. Historical background (Lorentz, Poincaré, Einstein)

The transformation in physical concepts which was brought about by the theory of relativity, had been in preparation for a long time. As long ago as 1887, in a paper still written from the point of view of the elastic-solid theory of light, Voigt¹ mentioned that it was mathematically convenient to introduce a local time t' into a moving reference system. The origin of t' was taken to be a linear function of the space coordinates, while the time scale was assumed to be unchanged. In this way the wave equation

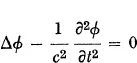
could be made to remain valid in the moving reference system, too. These remarks, however, remained completely unnoticed, and a similar transformation was not again suggested until 1892 and 1895, when H. A. Lorentz² published his fundamental papers on the subject. Essentially physical results were now obtained, in addition to the purely formal recognition that it was mathematically convenient to introduce a local time t' in a moving coordinate system. It was shown that all experimentally observed effects of first order in υ/c (ratio of the translational velocity of the medium to the velocity of light) could be explained quantitatively by the theory when the motion of the electrons embedded in the aether was taken into account. In particular, the theory gave an explanation for the fact that a common velocity of medium and observer relative to the aether has no influence on the phenomena, as far as quantities of first order are concerned.³

However, the negative result of Michelson’s interferometer experiment⁴, concerned as it was with an effect of second order in υ/c, created great difficulties for the theory. To remove these, Lorentz⁵ and, independently, FitzGerald put forward the hypothesis that all bodies change their dimensions when moving with a translational velocity υ. This change of dimension would be governed by a factor κ √[1 − (υ²/c²] in the direction of motion, with κ as the corresponding factor for the transverse direction; κ itself remains undetermined. Lorentz justified this hypothesis by pointing out that the molecular forces might well be changed by the translational motion. He added to this the assumption that the molecules rest in a position of equilibrium and that their interaction is purely electrostatic. It would then follow from the theory that a state of equilibrium exists in the moving system, provided all dimensions in the direction of motion are shortened by a factor √[1 − (υ²/c²], with the transverse dimensions unaltered. It now remained to incorporate this “Lorentz contraction” in the theory, as well as to interpret the other experiments⁶ which had not succeeded in showing the influence of the earth’s motion on the phenomena in question. There was first of all Larmor who, as early as 1900, set up the formulae now generally known as the Lorentz transformation, and who thus considered a change also in the time scale⁷. Lorentz’s review article⁸, completed towards the end of 1903, contained several brief allusions which later proved very fruitful. He conjectured that if the idea of a variable electromagnetic mass was extended to all ponderable matter, the theory could account for the fact that the translational motion would produce only the above-mentioned contraction and no other effects, even in the presence of molecular motion. This would also explain the Trouton and Noble experiment. In addition, he raised the important question whether the size of the electrons might be changed by the motion.⁹ However, in the introduction to his article, Lorentz still maintained the principle that the phenomena depended not only on the relative motion of the bodies, but also on the motion of the aether.^9a

We now come to the discussion of the three contributions, by Lorentz¹⁰, Poincaré¹¹ and Einstein¹², which contain the line of reasoning and the developments that form the basis of the theory of relativity. Chronologically, Lorentz’s paper came first. He proved, above all, that Maxwell’s eauations are invariant under the coordinate transformation¹³

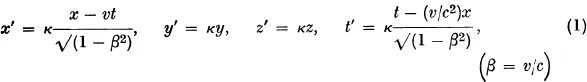
provided the field intensities in the primed system are suitably chosen. This, however, he proved rigorously only for Maxwell’s equations in charge-free space. The terms which contain the charge density and current are, in Lorentz’s treatment, not the same in the primed and the moving systems, because he did not transform these quantities quite correctly. He therefore regarded the two systems as not completely, but only very approximately, equivalent. By assuming that the electrons, too, could be deformed by the translational motion and that all masses and forces have the same dependence on the velocity as purely electromagnetic masses and forces, Lorentz was able to derive the existence of a contraction affecting all bodies (in the presence of molecular motion as well). He could also explain why all experiments hitherto known had failed to show any influence of the earth’s motion on optical phenomena. A less immediate consequence of his theory is that one has to put κ = 1. This means that the transverse dimensions remain unchanged during the motion, if indeed this explanation is at all possible. We would like to stress that even in this paper the relativity principle was not at all apparent to Lorentz. Characteristically, and in contrast to Eihstein, he tried to understand the contraction in a causal way.

The formal gaps left by Lorentz’s work were filled by Poincaré. He stated the relativity principle to be generally and rigorously valid. Since he, in common with the previously discussed authors, assumed Maxwell’s equations to hold for the vacuum, this amounted to the requirement that all laws of nature must be covariant with respect to the “Lorentz transformation”¹⁴. The invariance of the transverse dimensions during the motion is derived in a natural way from the postulate that the transformations which effect the transition from a stationary to a uniformly moving system must form a gro...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• Preface by A. Sommerfeld
• Bibliography
• Part I. The foundations of the special theory of relativity
• Part II. Mathematical tools
• Part III. Special theory of relativity. Further elaborations
• Part IV. General theory of relativity
• Part V. Theories on the nature of charged elementary particles
• Supplementary Notes
• Author Index
• Subject Index