100 Great Problems of Elementary Mathematics

Heinrich Dörrie

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486613482
• eBook ISBN: 9780486318479
• Topic: Mathematics
• Subtopic: Arithmetic
• Index: Mathematics

"The collection, drawn from arithmetic, algebra, pure and algebraic geometry and astronomy, is extraordinarily interesting and attractive." — Mathematical Gazette
This uncommonly interesting volume covers 100 of the most famous historical problems of elementary mathematics. Not only does the book bear witness to the extraordinary ingenuity of some of the greatest mathematical minds of history — Archimedes, Isaac Newton, Leonhard Euler, Augustin Cauchy, Pierre Fermat, Carl Friedrich Gauss, Gaspard Monge, Jakob Steiner, and many others — but it provides rare insight and inspiration to any reader, from high school math student to professional mathematician. This is indeed an unusual and uniquely valuable book.
The one hundred problems are presented in six categories: 26 arithmetical problems, 15 planimetric problems, 25 classic problems concerning conic sections and cycloids, 10 stereometric problems, 12 nautical and astronomical problems, and 12 maxima and minima problems. In addition to defining the problems and giving full solutions and proofs, the author recounts their origins and history and discusses personalities associated with them. Often he gives not the original solution, but one or two simpler or more interesting demonstrations. In only two or three instances does the solution assume anything more than a knowledge of theorems of elementary mathematics; hence, this is a book with an extremely wide appeal.
Some of the most celebrated and intriguing items are: Archimedes' "Problema Bovinum," Euler's problem of polygon division, Omar Khayyam's binomial expansion, the Euler number, Newton's exponential series, the sine and cosine series, Mercator's logarithmic series, the Fermat-Euler prime number theorem, the Feuerbach circle, the tangency problem of Apollonius, Archimedes' determination of pi, Pascal's hexagon theorem, Desargues' involution theorem, the five regular solids, the Mercator projection, the Kepler equation, determination of the position of a ship at sea, Lambert's comet problem, and Steiner's ellipse, circle, and sphere problems.
This translation, prepared especially for Dover by David Antin, brings Dörrie's "Triumph der Mathematik" to the English-language audience for the first time.

Arithmetical Problems

1 Archimedes’ Problema Bovinum

The sun god had a herd of cattle consisting of bulls and cows, one part of which was white, a second black, a third spotted, and a fourth brown.

Among the bulls, the number of white ones was one half plus one third the number of the black greater than the brown; the number of the black, one quarter plus one fifth the number of the spotted greater than the brown; the number of the spotted, one sixth and one seventh the number of the white greater than the brown.

Among the cows, the number of white ones was one third plus one quarter of the total black cattle; the number of the black, one quarter plus one fifth the total of the spotted cattle; the number of the spotted, one fifth plus one sixth the total of the brown cattle; the number of the brown, one sixth plus one seventh the total of the white cattle.

What was the composition of the herd?

SOLUTION. If we use the letters X, Y, Z, T to designate the respective number of the white, black, spotted, and brown bulls and x, y, z, t to designate the white, black, spotted, and brown cows, we obtain the following seven equations for these eight unknowns:

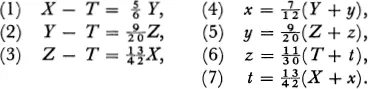
From equations (1), (2), (3) we obtain 6X – 5Y = 6T, 20Y – 9Z = 20 T, 42Z – 13X = 42 T, and taking these three equations as equations for the three unknowns X, Y, and Z, we find

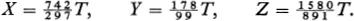
Since 891 and 1580 possess no common factors, T must be some whole multiple—let us say G—of 891. Consequently,

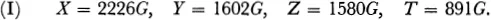
If these values are substituted into equations (4), (5), (6), (7), the following equations are obtained:

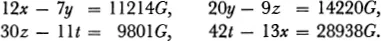
These equations are solved for the four unknowns x, y, z, t and we obtain

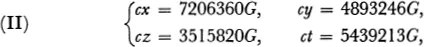
in which c is the prime number 4657. Since none of the coefficients of G on the right can be divided by c, then G must be an integral multiple of c:

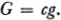
If this value of G is introduced into (I) and (II), we finally obtain the following relationships:

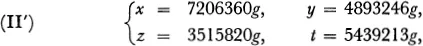
where g may be any positive integer.

The problem therefore has an infinite number of solutions. If g is assigned the value 1, we obtain the following:

HISTORICAL. As the above solution shows, the problem of the cattle cannot properly be considered a very difficult problem, at least in terms of present concepts. Since, however, in ancient times a difficult problem was frequently referred to specifically as a problema bovinum or else as a problema Archimedis, one may assume that the form of the problem dealt with above does not represent the complete and original form of Archimedes’ problem, especially when one considers the...

Table of contents

• Cover
• Title Page
• Copyright
• Contents
• Preface
• Arithmetical Problems
• Planimetric Problems
• Problems Concerning Conic Sections and Cycloids
• Stereometric Problems
• Nautical and Astronomical Problems
• Extremes
• Index of Names