Topology and Geometry for Physicists

Charles Nash, Siddhartha Sen, Siddhartha Sen

• Publisher: Dover Publications
• Year: 2013
• Topic: Mathematics
• eBook ISBN:
  9780486318363
• Subtopic: Topology
• Index: Mathematics

Differential geometry and topology are essential tools for many theoretical physicists, particularly in the study of condensed matter physics, gravity, and particle physics. Written by physicists for physics students, this text introduces geometrical and topological methods in theoretical physics and applied mathematics. It assumes no detailed background in topology or geometry, and it emphasizes physical motivations, enabling students to apply the techniques to their physics formulas and research.
"Thoroughly recommended" by The Physics Bulletin, this volume's physics applications range from condensed matter physics and statistical mechanics to elementary particle theory. Its main mathematical topics include differential forms, homotopy, homology, cohomology, fiber bundles, connection and covariant derivatives, and Morse theory.

CHAPTER 1

Basic Notions of Topology and the Value of Topological Reasoning

1.1 INTRODUCTION

Topology can be thought of as a kind of generalization of Euclidean geometry, and also as a natural framework for the study of continuity. Euclidean geometry is generalized by regarding triangles, circles, and squares as being the same basic object. Continuity enters because in saying this one has in mind a continuous deformation of a triangle into a square or a circle, or indeed any arbitrary shape. A disc with a hole in the centre is topologically different from a circle or a square because one cannot create or destroy holes by continuous deformations. Thus using topological methods one does not expect to be able to identify a geometrical figure as being a triangle or a square. However, one does expect to be able to detect the presence of gross features such as holes or the fact that the figure is made up of two disjoint pieces etc. This leads to the important point that topology produces theorems that are usually qualitative in nature—they may assert, for example, the existence or non-existence of an object. They will not in general, provide the means for its construction.

Let us begin by looking at some examples where topology plays a role.

Example 1. Cauchy’s residue theorem

Consider the contour integral for a meromorphic function f(z) along the path Γ₁ which starts at a and finishes at b (c.f. Fig. 1.1). Let us write

Now deform the path Γ₁ continuously into the path Γ₂ shown in Fig. 1.1. Provided we cross no poles of f(z) in deforming Γ₁ into Γ₂, then Cauchy’s theorem for meromorphic functions allows us straightaway to deduce that

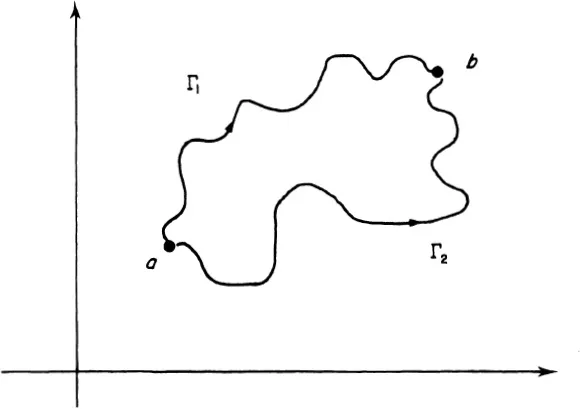
Figure 1.1

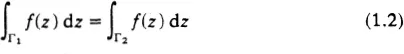
This is just the statement that

where C is the closed contour made up by joining Γ₁ to Γ₂ and reversing the arrow on Γ₁ so as to give an anticlockwise direction to the contour C. The intuitive content of this result is that to integrate f(z) from a to b in the complex plane is independent of the path joining a to b (under the conditions stated). Even if we relax these conditions and allow that the deformation of Γ₁ into Γ² may entail the crossing of some poles of f(z), then we still have complete knowledge of the relationship of the two integrals. It is simply

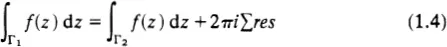
where the sum is over the residues, if any, of the poles inside C. This simple example uncovers some topological properties underlying the familiar Cauchy theorem.

Example 2. The fundamental theorem of algebra

In this example we shall use the Cauchy theorem to give a proof of the fundamental theorem of algebra. First of all a simple consequence of Cauchy’s theorem is that for a meromorphic function f(z) we have

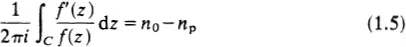
where n₀ and n_p are the number of zeroes and the number of poles respectively of f(z) lying inside C Let f(z) be the polynomial Q(z) of degree q where

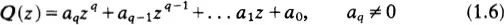
Then since Q(z) has no poles we have

It is clear that n₀ is a continuous function of q of the q + 1 coefficients a₀, . . ., a_q. Let us select the coefficients a₀, . . ., a_{q − 1} and write

However, n₀ also only takes integer values. Now since it is impossible to continuously jump from one integer value to another it follows that n₀ must be invariant under continuous change of the a_i’s. This state of affairs permits the following argument: for large |z|, say |z| > R, |Q(z)|, grows as |a_q||z|^q which is a large number. Then if C is a circ...

Table of contents

• Cover
• Title Page
• Dedication
• Contents
• Chapter 1. Basic Notions of Topology and the Value of Topological Reasoning
• Chapter 2. Differential Geometry: Manifolds and Differential Forms
• Chapter 3. The Fundamental Group
• Chapter 4. The Homology Groups
• Chapter 5. The Higher Homotopy Groups
• Chapter 6. Cohomology and De Rham Cohomology
• Chapter 7. Fibre Bundles and Further Differential Geometry
• Chapter 8. Morse Theory
• Chapter 9. Defects, Textures and Homotopy Theory
• Chapter 10. Yang-Mills Theories: Instantons and Monopoles
• Further Reading
• Subject Index