The Stanford Mathematics Problem Book

With Hints and Solutions

G. Polya, J. Kilpatrick

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486318325
• Topic: Mathematics
• Subtopic: Pre-Calculus
• Index: Mathematics

This volume features a complete set of problems, hints, and solutions based on Stanford University's well-known competitive examination in mathematics. It offers high school and college students an excellent mathematics workbook of rigorous problems that will assist in developing and cultivating their logic and probability skills.These 20 sets of intriguing problems test originality and insight rather than routine competence. They involve theorizing and verifying mathematical facts; examining the results of general statements; discovering that highly plausible conjectures can be incorrect; solving sequences of subproblems to reveal theory construction; and recognizing `red herrings,` in which obvious relationships among the data prove irrelevant to solutions. Hints for each problem appear in a separate section, and a final section features solutions that outline the appropriate procedures.Ideal for teachers seeking challenging practice math problems for their gifted students, this book will also help students prepare for mathematics, science, and engineering programs. Mathematics buffs of all ages will also find it a source of captivating challenges.

Part One

INTRODUCTION

For twenty years, from 1946 to 1965, the Department of Mathematics at Stanford University conducted a competitive examination for high school seniors. The immediate and principal purpose of the examination was to identify, among each year's high school graduates, singularly capable students and attract them to Stanford. The broader purpose was to stimulate interest in mathematics among high school students and teachers generally, as well as the public.

The examination was modeled on the Eötvös Competition [see 23],° which was organized in Hungary in 1894 and which, in turn, appears to have been suggested by similar competitions in England and France. Gabor Szegö, chairman of the Stanford Department of Mathematics in 1946 and winner of the Eötvös Competition in 1912, initiated the Stanford examination.

The examination was established in the belief that an early manifestation of mathematical ability is a definite indication of exceptional intelligence and suitability for intellectual leadership in any field of endeavor. Furthermore, mathematical ability can be tested at a comparatively early age because it is manifested “not so much by the amount of accumulated knowledge as by the originality of mind displayed in the game of grappling with difficult though elementary problems [2, p. 406].”

As Buck [1] noted some years ago in reviewing mathematical competitions, an examination can be designed, broadly speaking, to test either achievement or aptitude. The Stanford University Competitive Examination in Mathematics was of the latter type. It emphasized

originality and insight rather than routine competence.... A typical question might call for specific knowledge within the reach of those being tested, but would call for the employment of this in unusual ways requiring a high degree of ingenuity. The question may in fact introduce certain concepts which are quite unfamiliar to the student. In short, the winning student is asked to demonstrate research ability [1, pp. 204–205].

The first Stanford examination, in 1946, was administered in 60 California high schools to 322 participants. The winner was awarded a one-year scholarship by Stanford University; honorable mention and a mathematics book were given to three other participants. In 1953, the examination was extended beyond California to include Arizona, Oregon, and Washington; the number of scholarships was increased to two; and the number of honorable mention awards and books was increased to ten or so. From 1958 to 1962, the examination was co-sponsored by Sylvania Electric Products, Inc. The last examination, in 1965, was administered to about 1200 participants in 151 centers in California, Arizona, Idaho, Montana, Nevada, Oregon, and Washington. Cash prizes of $500, $250, and $250 were awarded to the three winners; honorable mention and a mathematics book went to eighteen participants. The examination was discontinued after 1965 mainly because the Stanford Department of Mathematics turned its interest to more graduate teaching.

Announcements of the examination were sent each year to all public and private high schools in each state where the examination was to be administered. Larger schools were designated as centers; students from other schools were free to arrange to take the examination in a convenient location.

The examination was administered by teachers and school personnel on a Saturday afternoon in March or April. The participants were given three hours to attempt three to five problems. The following instructions were, given:

No books or notebooks may be used. You may not be able to do all the problems in three hours, but whatever you do should be carefully thought out. Scratch paper may be used. Either pen or pencil may be used. No questions concerning the test should be asked of the person in charge.

Good presentation counts!

It should be clear, concise, complete.

The papers were read in a two-stage process: First, they were read by teams of graduate students in the Department of Mathematics, including, as was sometimes possible, graduate students who were experienced high school teachers. Each team of two students was assigned a problem to read in as many papers as they could handle. Papers containing either a stated minimum of good solutions (for example, one and a half or two out of four) or some special feature were forwarded to the second stage. In the second stage, each paper that survived the first screening was read by at least one faculty member of the Department. The papers considered most likely to be winners were read by all participating faculty members.

To make the selection of winners easier, the problems were devised so that only a very few participants would be able to solve all of them. On the other hand, to avoid too much frustration, the first problem was usually more accessible than the others, especially in the later years, so that many participants were able to solve it.

Although the mathematical content of the problems did not go beyond that of the high school curriculum, the problems were of types seldom found in textbooks. The purpose of such problems was not only to test the students’ originality, but also to enrich the high school mathematics program by suggesting some new directions for students’ and teachers’ work. The types of problems included: (1) “guess and prove,” in which one first guesses and then proves a mathematical fact; (2) “test consequences,” in which one tests the consequences of a general statement; (3) “you may guess wrong,” in which a highly plausible guess is incorrect; (4) “small scale theory,” in which a sequence of subproblems illustrates theory construction; and (5) “red herring,” in which an obvious relationship among the data turns out to be irrelevant to the solution [see 9; 19, pp. 160–161, ex. 1; 21, p. 139, ex. 14.23].

The problems were of the sort used as illustrations in How to Solve It[17], in the two volumes of Mathematics and Plausible Reasoning [18, 19], and in the two volumes of Mathematical Discovery [20, 21]. In fact, many of the problems appear, usually with solutions, in one or another of those books.

Most of the problems have also appeared in journals. The problems and the list of winners for each examination from 1946 to 1953 (except 1952) were published in the American Mathematical Monthly [2, 3, 4, 5, 6, 7, 8]; and the complete set of problems, together with an Introduction, somewhat adapted here, appears in the June–July 1973 issue of that monthly [24]. Articles containing problems, solutions, comments, and lists of winners for 1953 to 1961 (except 1959) were published in the California Mathematics Council Bulletin [9, 10, 11, 12, 13, 14, 15, 16].

The complete set of problems has never before, however, been published together with hints and solutions for all problems. Material copyrighted previously is reprinted here by permission.

Part Two contains the complete set of problems from the Stanford University Competitive Examination in Mathematics. They are numbered sequentially, by year and problem number, as follows: 46.1 designates problem 1 in the 1946 examination.

Part Three contains a hint for each problem; the hints are numbered to correspond with the problems. The hints are similar to those in Part IV of How to Solve It [17], and most of them use one or more of the heuristic questions and suggestions treated in that book.

Part Four contains a solution for each problem (sometimes two solutions); the numbering is as before. Solutions outline the procedures used, but some details are, of course, left to the reader. Some solutions end with an indication of connections to other problems or generalizations.

References to articles and books in which problems have appeared previously (with or without solutions) are given in brackets with the corresponding solutions in Part Four.

Many of the hints and solutions have come from discussions in seminars on problem solving held at Stanford University and at Teachers College. The problems have been used to illustrate problem-solving techniques with freshmen, prospective teachers, and experienced teachers alike. Teachers, and teachers of teachers, may find some useful suggestions on how to use the problems in Mathematical Discovery [20, pp. 209–212].

---

^* Numbered references are on 67–68

Part Two

PROBLEMS

PROBLEMS 46

46.1. In a tennis tournament there are 2n participants. In the first round of the tournament each participant plays just once, so there are n games, each occupying a pair of players. Show that the pairing for the first round can be arranged in exactly

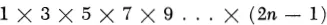
different ways.

46.2. In a tetrahedron (which is not necessarily regular) two opposite edges have the same length a and they are perpendicular to each other. Moreover they are each perpendicular to a line of length b which joins their midpoints. Express the volume of the tetrahedron in terms of a and b, and prove your answer.

46.3. Consider the following four propositions, which are not necessarily true.

I. If a polygon inscribed in a circle is equilateral it is also equiangular.

II. If a polygon inscribed in a circle is equiangular it is also equilateral.

III. If a polygon circumscribed about a circle is equilateral it is also equiangular.

IV. If a polygon circumscribed about a circle is equiangular it is also equilateral.

(A) State which of the four propositions are true and which are false, giving a proof of your statement in each case.

(B) If, instead of general polygons, we should consider only quadrilaterals which of the four propositions are true and which are false? And if we consider only pentagons?

In answering (B) you may state conjectures, but prove as much as you can and separate clearly what is proved and what is not.

PROBLEMS 47

47.1. To number the pages of a bulky volume the printer used 1890 digits. How many pages has the volume?

47.2. Among grandfather’s papers a bill was found:

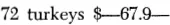
The first and last digit of the number that obviously represented the total price of those fowls are replaced here by blanks, for they have faded and are now illegible.

What are the two faded digits and what was the price of one turkey?

47.3. Determine m so that the equation in x

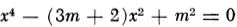
has four real roots in arithmetic progression.

47.4. Let α, β, and γ denote the anglęs of a triangle. Show that

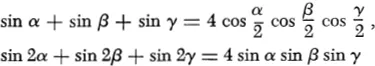
and

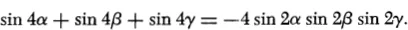
PROB...