Differential Manifolds

Antoni A. Kosinski

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486462448
• eBook ISBN: 9780486318158
• Topic: Mathematics
• Subtopic: Differential Geometry
• Index: Mathematics

The concepts of differential topology form the center of many mathematical disciplines such as differential geometry and Lie group theory. Differential Manifolds presents to advanced undergraduates and graduate students the systematic study of the topological structure of smooth manifolds. Author Antoni A. Kosinski, Professor Emeritus of Mathematics at Rutgers University, offers an accessible approach to both the h-cobordism theorem and the classification of differential structures on spheres.
"How useful it is," noted the Bulletin of the American Mathematical Society, "to have a single, short, well-written book on differential topology." This volume begins with a detailed, self-contained review of the foundations of differential topology that requires only a minimal knowledge of elementary algebraic topology. Subsequent chapters explain the technique of joining manifolds along submanifolds, the handle presentation theorem, and the proof of the h-cobordism theorem based on these constructions. There follows a chapter on the Pontriagin Construction—the principal link between differential topology and homotopy theory. The final chapter introduces the method of surgery and applies it to the classification of smooth structures of spheres. The text is supplemented by numerous interesting historical notes and contains a new appendix, "The Work of Grigory Perelman," by John W. Morgan, which discusses the most recent developments in differential topology.

VI

Operations on Manifolds

In this chapter we describe various operations on manifolds: connected sum, attachment of handles, and surgery. All of these are special cases of a general construction, joining of two manifolds along a submanifold, presented in Sections 4 and 5. However, since all important features are already present in the special cases of connected sum and connected sum along the boundary, we discuss these two cases first in Sections 1 and 3, respectively.

The general construction is specialized to attaching of handles in Section 6. We are particularly interested in the question when the attachment of two handles of consecutive dimensions results in no change to the manifold, that is when the second handle “destroys” the first. The main result in this direction, Smaleès Cancellation Lemma, is proved in Section 7. The proof is based on an elementary but far-reaching theorem concerning attachment of disc bundles along a cross section in the boundary.

In Section 8 we look at handle attachment from a different point of view, more convenient for homology calculations. Section 9 introduces the operation of surgery, and in Section 10 we calculate some related homological results. In Section 11 we define handlebodies and investigate their structure. Some important examples are constructed in Section 12 using the plumbing construction. The results of the last two sections will not be used until Chapter VIII.

1 Connected Sum

Connected sum is the operation of “joining two manifolds by a tube.”

Given two connected m-dimensional manifolds M₁, M₂, let h_i,: R^m → M_i, i = 1, 2, be two imbeddings. If both manifolds are oriented, then we assume that h₁ preserves the orientation and h₂ reverses it.

Let α : (0, ∞) → (0, ∞) be an arbitrary orientation reversing diffeomorphism. We define α_m: R^m − 0 → R^m − 0 by

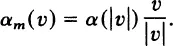
The connected sum M₁ # M₂(h₁, h₂, α) is the space obtained from the (disjoint) union of M₁ − h₁(0) and M₂ − h₂(0) by identifying h₁(υ) with h₂(α_M(υ)) ...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Contribution
• Contents
• Introduction
• I. Differentiable Structures
• II. Immersions, Imbeddings, Submanifolds
• III. Normal Bundle, Tubular Neighborhoods
• IV. Transversality
• V. Foliations
• VI. Operations on Manifolds
• VII. Handle Presentation Theorem
• VIII. The h-Cobordism Theorem
• IX. Framed Manifolds
• X. Surgery
• Appendix I
• Appendix II
• Bibliography
• Index