Fundamentals of Modern Mathematics

A Practical Review

David B. MacNeil

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486497457
• eBook ISBN: 9780486316147
• Topic: Mathematics
• Subtopic: Mathematics in Education
• Index: Mathematics

Students and others wishing to know a little more about the practical side of mathematics will find this volume a highly informative resource. An excellent supplement to college and high school courses as well as a guide to independent study, the book covers examples of pure mathematics as well as concepts of applied mathematics useful for solving problems that arise in business, industry, science, and technology.
Contents include examinations of the theory of sets, numbers and groups; matrices and determinants; probability, statistics, and quality control; and game theory. Additional subjects include inequalities, linear programming, and the transportation problem; combinatorial mathematics; transformations and transforms; and numerical analysis. Accessible explanations of important concepts feature a total of more than 150 diagrams and graphs, in addition to worked-out examples with step-by-step explanations of methods. Answers to exercises and problems appear at the end.

Chapter 1

THEORY OF SETS, NUMBERS, AND GROUPS

One of the most striking developments in modern mathematics has been the growth in importance of set theory. The reason for this development has been the fact that the entities or objects that are treated in every, or nearly every, branch of mathematics may be considered to be particular sets of entities or objects, so that their properties may be developed from general axioms of set theory. While to derive every branch of mathematics from set theory would be an extremely complex undertaking, there are sufficient basic applications of set theory, even at the level of this book, to justify its presentation in the opening chapter.

The concept of a set is intuitive, and is interchangeable with a class or a collection. The objects, or using the mathematical terms, the members or elements of the set may be of any sort. Thus there is the set of all birds, or the set of all Swedes. Mathematicians are more interested in such sets as the set of all prime numbers, or the set of all real numbers, or the set of regular polygons, or the set composed of −1, 0, and 1, or other sets of mathematical objects.

The procedure in the development of set theory is axiomatic, and it makes use of a distinctive symbolism. The meanings of the symbols are carefully defined. The entire structure of set theory is based on strictly logical inferences from the axioms, and requires some care at the start in learning the symbols and axioms. For that reason the number of symbols used in this chapter has been kept to a minimum, by stating in words those relations which occur less frequently.

1. Set Membership.The basic concept of set theory is that of set membership. If x is a member of the set A, this fact is expressed as

Here set membership is expressed by the symbol ∈, while the lower case letter x is used for the member and the capital letter A is used for the set. This use of lower case and capital letters cannot always be followed, however, since the members of a set may themselves be sets, which when so considered, become subsets.

2. Equality.The second concept, important here as in all mathematics, is that of equality. The relation of equality between set A and set B which is expressed as

is defined by the Axiom of Extentionality, as follows:

(1) Two sets are equal if and only if they have the same members, i.e., sets A and B are equal if and only if every member of set A is a member of set B, and every member of set B is a member of set A.

In order to determine whether or not two sets are equal, we must know their members. The members of a set may be expressed in two ways: by listing them or by describing them. For example, consider the set D, which has as its members a, b, c, and d. We can list the set D as

or we can describe it as

The braces are commonly used to enclose the list or the description. The description reads “a is a member of (set) D: a being specified as one or another of the first four letters of the alphabet.”

When one uses this second form of designating set membership, set description, he is said to specify the condition under which the elements of the set are determined. This method leads logically to the Axiom of Specification. Using the letter D for the four-member set in the above example, and the letter A for the set of all the letters of the alphabet, the Axiom of Specification would be stated as:

(2) To every set A and every condition S(x), there corresponds a set D having as members exactly those members x of A for which S(x) holds.

In the application, S(x) is the condition that the members of set D be just those members of A (A being the set of letters of the alphabet) for which S(x) holds, S(x) being the specification that x be one or another of the first four letters of the alphabet.

The foregoing would be written as:

3. Sets, Subsets and Inclusion.In the foregoing example, the set D of the first four letters of the alphabet, was a subset of the set A of all the letters of the alphabet, because A includes all the members of D. This relationship is symbolized as:

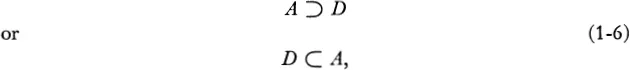
the open end of the symbol being turned away from the subset. Note that the set in which the subset is included may not contain any other members than those in the subset; in other words the subset may be equa...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• Chapter 1 Theory of Sets, Numbers and Groups
• Chapter 2 Matrices and Determinants
• Chapter 3 Probability, Statistics, and Quality Control
• Chapter 4 The Theory of Games
• Chapter 5 Inequalities, Linear Programming, and the Transportation Problem
• Chapter 6 Combinatorial Mathematics
• Chapter 7 Transformations and Transforms
• Chapter 8 Numerical Analysis
• Answers to Exercises and Problems
• Index