Fourier Series

G. H. Hardy, W. W. Rogosinski, W. W. Rogosinski

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486406817
• eBook ISBN: 9780486316284
• Topic: Mathematics
• Subtopic: Trigonometry
• Index: Mathematics

Geared toward mathematicians already familiar with the elements of Lebesgue's theory of integration, this classic, graduate-level text begins with a brief introduction to some generalities about trigonometrical series. Discussions of the Fourier series in Hilbert space lead to an examination of further properties of trigonometrical Fourier series, concluding with a detailed look at the applications of previously outlined theorems. Ideally suited for both individual and classroom study.

IV. CONVERGENCE OF FOURIER SERIES

4.1. Introduction. We have already proved one or two theorems concerning the convergence of the F.s. of functions of special types. In this chapter we discuss the problem of convergence more systematically.

One preliminary remark is advisable. The ‘convergence problem’ seems at first sight the central and most natural problem of the theory, and it was the first to be discussed seriously, but it has lost a good deal of its importance as the result of later research. A series may ‘converge’ in many senses, of which the classical sense of Cauchy is only one; and some of these senses, such as the ‘strong convergence’ of Ch. II and the ‘summability’ of Ch. v, can be correlated more naturally with the most obvious characteristics of the generating function.

We denote the partial sum of T(ƒ) by s_n(θ) or s_n(θ, ƒ). We write

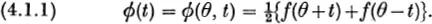
The ‘natural’ sum for T(ƒ) is ϕ (+ O), when this limit exists (as it does, for example, at a point of continuity or jump). The F.c. of ϕ(t), considered as a function of t, are A_n(θ) and 0, by Theorem 26; and the F.s. of ƒ(t), for t = θ, is the F.s. of ϕ(t), which is a cosine series in t, for t = 0. This remark enables us, if we wish, to reduce any convergence problem for a F.s., at the point θ, to the special case in which θ = 0 and the series is a cosine series.

4.2. The convergence problem for the Fourier series.

We have

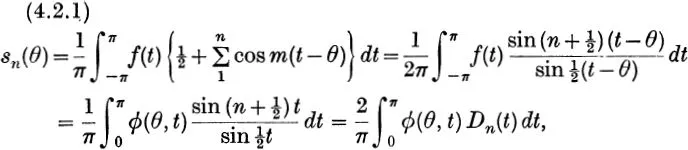
D_n(t), ‘Dirichlet's kernel’, being d...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Notations
• I. Generalities
• II. Fourier series in Hilbert space
• III. Further properties of trigonometrical Fourier series
• IV. Convergence of Fourier series
• V. Summability of Fourier series
• VI. Applications of the theorems of Chapter v
• VII. General trigonometrical series
• Notes