A First Course in Graph Theory

Gary Chartrand, Ping Zhang, Ping Zhang

• Publisher: Dover Publications
• Year: 2013
• eBook ISBN: 9780486297309
• Topic: Mathematics
• Subtopic: Discrete Mathematics
• Index: Mathematics

This comprehensive text offers undergraduates a remarkably student-friendly introduction to graph theory. Written by two of the field's most prominent experts, it takes an engaging approach that emphasizes graph theory's history. Unique examples and lucid proofs provide a sound yet accessible treatment that stimulates interest in an evolving subject and its many applications.
Optional sections designated as "excursion" and "exploration" present interesting sidelights of graph theory and touch upon topics that allow students the opportunity to experiment and use their imaginations. Three appendixes review important facts about sets and logic, equivalence relations and functions, and the methods of proof. The text concludes with solutions or hints for odd-numbered exercises, in addition to references, indexes, and a list of symbols.

Chapter 1

Introduction

1.1 Graphs and Graph Models

A major publishing company has ten editors (referred to by 1, 2, …, 10) in the scientific, technical and computing areas. These ten editors have a standard meeting time during the first Friday of every month and have divided themselves into seven committees to meet later in the day to discuss specific topics of interest to the company, namely, advertising, securing reviewers, contacting new potential authors, finances, used and rented copies, electronic editions and competing textbooks. This leads us to our first example.

Example 1.1 The ten editors have decided on the seven committees: c₁ = {1, 2, 3}, c₂ = {1, 3, 4, 5}, c₃ = {2, 5, 6, 7}, c₄ = {4, 7, 8, 9}, c₅ = {2, 6, 7}, c₆ = {8, 9, 10}, c₇ = {1, 3, 9, 10}. They have set aside three time periods for the seven committees to meet on those Fridays when all ten editors are present. Some pairs of committees cannot meet during the same period because one or two of the editors are on both committees. This situation can be modeled visually as shown in Figure 1.1.

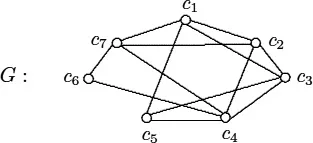
Figure 1.1: A graph

In this figure, there are seven small circles, representing the seven committees and a straight line segment is drawn between two circles if the committees they represent have at least one committee member in common. In other words, a straight line segment between two small circles (committees) tells us that these two committees should not be scheduled to meet at the same time. This gives us a picture or a “model” of the committees and the overlapping nature of their membership.

What we have drawn in Figure 1.1 is called a graph. Formally, a graph G consists of a finite nonempty set V of objects called vertices (the singular is vertex) and a set E of 2-element subsets of V called edges. The sets V and E are the vertex set and edge set of G, respectively. So a graph G is a pair (actually an ordered pair) of two sets V and E. For this reason, some write G = (V, E). At times, it is useful to write V(G) and E(G) rather than V and E to emphasize that these are the vertex and edge sets of a particular graph G. Although G is the common symbol to use for a graph, we also use F and H, as well as G′, G″ and G₁, G₂, etc. Vertices are sometimes called points or nodes and edges are sometimes called lines. Indeed, there are some who use the term simple graph for what we call a graph. Two graphs G and H are equal if V(G) = V(H) and E(G) = E(H), in which case we write G = H.

It is common to represent a graph by a diagram in the plane (as we did in Figure 1.1) where the vertices are represented by points (actually small circles – open or solid) and whose edges are indicated ...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication
• Contents
• Preface
• 1. Introduction
• 2. Degrees
• 3. Isomorphic Graphs
• 4. Trees
• 5. Connectivity
• 6. Traversability
• 7. Digraphs
• 8. Matchings and Factorization
• 9. Planarity
• 10. Coloring Graphs
• 11. Ramsey Numbers
• 12. Distance
• 13. Domination
• Appendix 1. Sets and Logic
• Appendix 2. Equivalence Relations and Functions
• Appendix 3. Methods of Proof
• Solutions and Hints for Odd-Numbered Exercises
• References
• Index of Names
• Index of Mathematical Terms
• List of Symbols
• Back Cover