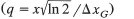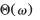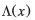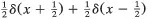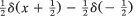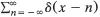Deconvolution of Images and Spectra

Second Edition

Peter A. Jansson

• Publisher: Dover Publications
• Year: 2014
• eBook ISBN: 9780486294452
• Topic: Technology & Engineering
• Subtopic: Engineering General
• Index: Technology & Engineering

Deconvolution is a technique in signal or image processing that is applied to recover information. When it is employed, it is usually because instrumental effects of spreading and blurring have obscured that information. In 1996, Deconvolution of Images and Spectra was published (Academic Press) as a second edition of Jansson's 1984 book, Deconvolution with Applications in Spectroscopy. This landmark volume was first published to provide both an overview of the field, and practical methods and results.
The present Dover edition is a corrected reprinting of the second edition. It incorporates all the advantages of its predecessors by conveying a clear understanding of the field while providing a selection of effective, practical techniques. The authors assume only a working knowledge of calculus, and emphasize practical applications over topics of theoretical interest, focusing on areas that have been pivotal to the evolution of the most effective methods. This tutorial is essentially self-contained. Readers will find it practical and easy to understand.

Chapter 1 | Convolution and Related Concepts

Peter A. Jansson

College of Optical Sciences, University of Arizona, Tucson

I. Introduction

II. Definition of Convolution

A. Discrete Case

B. Continuous Case

III. Properties

A. Integration and Differentiation

B. Central-Limit Theorem

C. Voigt Function

IV. Fourier Transforms

A. Special Symbols and Useful Functions

B. Some Properties and Relationships

C. Sampling and the Discrete Fourier Transform

D. Hartley Transform

V. The Problem of Deconvolution

A. Defining the Problem

B. Difficulties

C. Alternatives to Deconvolution

References

List of Symbols

a, b, g	functions a(x), b(x), g(x), with no explicit dependences shown
a',b',g'	first derivatives of functions a, b,g
an,bn,gn,	sampled values of a(x), b(x), g(x)
a(x), b(x), g(x)	functions used to illustrate properties of convolution
A,B,G	functions A(ω), B(ω), C(ω), with no explicit dependences shown
A(ω), B(ω), G(ω)	Fourier transforms of a(x), b(x), g(x)
c	Constant
C	Constant
cas(x)	Cos(x)+Sin(x)
f(x),F(ω)	function and Fourier transform, respectively
F'(ω), F"(ω)	first and second derivatives of F(ω), respectively
G(ζ)	Fourier transform of g(x) give n by alternative convention
H(X)	1 when x>0, 0 when x≤0
i(x),i	"image" data that incorporate smearing by s(x); sometimes include noise
ip(x)	ideal noise-free image data
îM(υ,x)	model representing idealized image data
j	imaginary operator such that j2 = -1
n(x)	additive noise
Na,Nb,Ng	number of samples available for function a,b,g
o(x),o	"object" or function sought by deconvolution, usually the true spectrum, but also the instrument function when this is sought by deconvolution
ô(x)	estimate of o(x)
ôM(υ,x)	model of true spectrum or true object
q	independent variable given in scaled units of Gaussian halfwidths
rect(x)	rectangle function having haif-width ½
sgn(x)	1 when x>0, -1 when x≤0
sinc(x)	(sin πx)/πx
Si(x)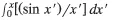
s(x),s	spread function, usually the instrument function, but also spreading due to other causes
s(x,x')	general integral equation kernel; shift-variant spread function
υ(x)	function used to illustrate Fourier transform
V(ω)	Fourier transform of υ(x) given by third system
x,x'	generalized independent variables and arguments of various functions
〈x〉,〈x2〉	first and second moments of a distribution of x
z(x)z1(x),z2(x)	functions used to illustrate the Hartley transform
z(ω)z1(ω ),z2(ω )	Hartley transforms of z(x), z1(x), and z2(x), respectively
z2e(ω)z20(ω)	even and odd parts of Z2(ω)
®	fractional increase in instrument response-function breadth due to convolution with narrow spectral line
β	parameter specifying influence of sharpness or smoothness criteria
⊗	convolution operation
δ(x),δ	Dirac δ function or impulse
δ'(x),δ'	first derivative of δ(x)
Δ(x)	half-width at half maximum (HWHM)
ΔxG,ΔxC	Gaussian and Cauchy half-widths at half maximum
ΔxN	Nyquist interval
ζ	conjugate of x in alternative Fourier transform system; Fourier frequency in cycles per units of x; variable of integration
θ(x),	spurious part of solution ô(x) and its Fourier transform Ô(ω)
	triangle function of unit height and half-width ½
μ	scaled ratio of Cauchy to Gaussian half-widths,
σ	standard deviation
σ^2	variance
σ^2a,σ^2b,σ^2g	variances of a, b,g
σ^2A,σ^2B,σ^2G	variances of A,B,G
τ(ω ),τ	τ(ω ), Fourier transform of s(x)
υ	vector having components υl
υ1	parameters of a model comprising multiple peaks
Φ(υ)	objective function to be minimized
ω	conjugate of x; Fourier frequency in radians per units of x
Ω	cutoff frequency such that τ(ω) = 0 for |ω| > Ω
II(x)	positive-impulse pair
II(x)	impulse pair with positive and negative components,
III(x)	Dirac “comb”

I. Introduction

Our daily experience abounds with phenomena that can be described mathematically by convolution. Spreading, blurring, and mixing are qualitative terms frequently used to describe these phenomena. Sometimes the spreading is caused by physical occurrences unrelated to our mechanisms of perception; sometimes our sensory inputs are directly involved. The blurred visual image is an example that comes to mind. The blur may exist in the image that the eye views, or it may result from a physiological defect. Biological sensory perception has parallels in the technology of instrumentation. Like the human eye, most instruments cannot discern the finest detail. Instruments are frequently designed to determine some observable quantity while an independent parameter is varied. An otherwise isolated measurement is often corrupted by undesired contributions that should rightfully have been confined to neighboring measurements. When such contributions add up linearly in a certain way, the distortion may be described by the mathematics of convolution.

Spectroscopy is profoundly affected by these spreading and blurring phenomena. The recovery of a spectrum as it would be observed by a hypothetical, perfectly resolving instrument is an exciting goal. Recent advances have stimulated development of restoring methods that r...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Preface
• 1 Convolution and Related Concepts
• 2 Distortion of Optical Spectra
• 3 Traditional Linear Deconvolution Methods
• 4 Modern Constrained Nonlinear Methods
• 5 Convergence of Relaxation Algorithms
• 6 Instrumental Considerations
• 7 Deconvolution Examples
• 8 Application to Electron Spectroscopy for Chemical Analysis
• 9 Deconvolution in Optical Microscopy
• 10 Deconvolution of Hubble Space Telescope Images and Spectra
• 11 Maximum Probable Estimates of Spectra
• 12 Fourier Spectrum Continuation
• 13 Minimum-Negativity-Constrained Fourier Spectrum Continuation
• 14 Alternating Projections onto Convex Sets
• Index