Ingenious Mathematical Problems and Methods

Louis A. Graham

• Publisher: Dover Publications
• Year: 2013
• eBook ISBN: 9780486282930
• Topic: Mathématiques
• Subtopic: Jeux en mathématiques

For two decades, an international readership of workers in applied mathematics submitted their favorite puzzles to a mid-twentieth-century column, The Graham Dial. This original collection features 100 of the publication's very best problems, with themes ranging from logic and engineering situations to number theory and geometry. Each problem was specifically selected for its widely differing modes of solution, and most include several methods of solution plus assessments of their efficacy.
In checking their solutions against the book's, readers may find that their interest in the puzzles increases. The search for an answer can develop into a challenge to improve upon existing solutions, as in a friendly competition among dozens of keen-witted, problem-solving engineers and mathematical puzzle fans. More than two dozen "mathematical nursery rhymes" appear throughout the book, which concludes with a final section of 25 "quickies" that will test readers' speed.

25 CHALLENGING QUICKIES

THESE ARE SELECTED for their special interest from the “Companion Puzzlers” that accompany the longer problems in most issues of the DIAL. Readers are invited to keep track of the time taken to reach the solution to these quickies, which should not normally exceed five minutes, since most of them are chiefly a test of mental agility in finding the best short-cut to the answer.

76. BALLS IN THE BOX

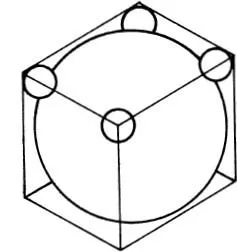
Fig. 45

A manufacturer of steel balls shipped his 2″ balls individually in a lined cubical box with inside dimensions of substantially 2″ to assure a snug fit. It occurred to him that he might use the space at the top four corners to carry four additional balls that would fit snugly against the big ball, two sides of the box and the box top. What would be the approximate diameter of the four small balls?

77. THE FOUR-CUSHION SHOT

Murray S. Klamkin, Brooklyn, tells of a billiard player who hit a ball with no “English” in such a way that it returned to its starting point after hitting four different cushions. How far did it travel?

78. SUM OF THE CUBES

Dr. Ernest Rabinowicz, M.I.T., invites you to find quickly any two different integers, the sum of whose cubes is the fourth power of an integer. And, after finding one pair of numbers that fill the bill, tell how you could find all such cases.

79. THE GRAZING COWS

Mr. Richard C. Eggleston, Coles Laboratories, Signal Corps, Monmouth Beach, N. J., tells of a farmer who had an extensive grazing area for his cows, the grass yield being uniform throughout, as was its consumption by each of the animals. Eight of his herd consumed the original grass and new growth on a two-acre plot in two weeks, after which he moved them to a fresh two-acre plot, which lasted them three weeks more. During this same five-week period another group of cows was making short of a five-acre plot. How many cows were in that group?

80. THE WOBBLY WHEEL

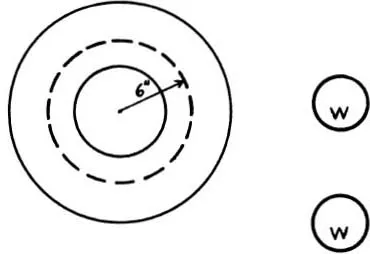
Fig. 46

Mr. David A. Lee, AiResearch Manufacturing Company, Los Angeles, Cal., tells of a mechanic who had a wheel that was pretty badly out of balance. All he had on hand to reduce the unbalance was two equal weights, each weighing an integral number of pounds. Each weight could be fastened at any desired point six inches from the center of the wheel, whose shaft would be supported on knife edges while making the static correction. At what two points should the weights be fastened, one after the other, to do the job? And if the unbalance were six inch-pounds and the weights two pounds each; how far apart would they be placed?

81. OLD MAN AND HIS SON

W. W. Johnson, of Cleveland, writes, “An old man and his son make a 64-mile trip with their saddle horse which travels 8 miles per hour but can carry only one person at a time. The man can walk 3 miles in one hour and the son 4 miles. They alternately ride and walk. Each one ties the horse after riding a certain distance, and then walks ahead, leaving the horse tied for the other’s arrival. At the halfway point they come together and take one half-hour for lunch and to feed the horse. At what time do they arrive at their destination if they start at 6 A.M.?”

82. SHEET OF PAPER

A. W. Everest, General Electric Co., Pittsfield, Mass., invites you to cut a sheet of typewriter paper into three pieces which can be rearranged into a square; prove your solution.

83. EARLIEST TIE FOR THE PENNANT

In May, 1955, when the Dodgers had won so many of their early games as to make it seem a runaway race for the National League pennant, Mr. D. R. Chicoine, Project Engineer, A. E. Staley Mfg. Co., Decatur, was inspired to make this provocative query: “What is the earliest point in a regulation major-league baseball schedule that a team can be assured at least a tie for first place in the final standings?”

84. ALL FOUR AILMENTS

This one, contributed by Norman Anning, Ann Arbor, is a rather unique test of alertness of thought: “If 70% of the population have stomach trouble, 75% have weak eyes, 80% have a liver ailment, and 85% have a touch of catarrh; what per cent at least are plagued with all four ailments?”

85. DELETED CHECKERBOARD

Fig. 47

Robert S. Raven, Westinghouse, Cleveland, offers this unique poser: “Two diagonally opposite corner squares are cut out from a checkerboard. The checkerboard now has an area of 62 squares. You are supplied with 31 identical dominoes with dimensions two squares by one square. The total area of the dominoes is thus also 62 squares. It is now proposed to cover the deleted board completely with non-overlapping dominoes. Prove this is possible or impossible in one or two sentences.”

MATHEMATICAL NURSERY RHYME No. 22

Tom, Tom, the piper’s son,

Could pipe as pert as any one

In longitudinal waves of strength

With frequency inverse to length.

And every blast, when he’d begin it,

Blared out at thirteen miles a minute.

MATHEMATICAL NURSERY RHYME No. 23

If a pair of shorts you need

Pythagoras is the man to heed.

Layout the squares per sketch above;

If you like Euclid, this you’ll love.

Then simply cut the pants to fit. —

You’ll be the latest fashion hit.

MATHEMATICAL NURSERY RHYME No. 24

“O shade of Bernoulli, tell me truly,

How did your numbers grow?

“With B’s and C’s and a sprinkle of e’s

And factorials all in a row.”

MATHEMATICAL NURSERY RHYME No. 25

Old Mother Hubbard went to the cupboard

To stop her poor doggie’s sad whine.

Algebraically speaking, the food she was seeking

Made the look on her k9b9.

MATHEMATICAL NURSERY RHYME No. 26

Fiddle de dum, fiddle de dee,

A young man sat beneath a tree

And pondered over gravity:

“Cm sub one times m sub two

Divided by d squared, ’tis true,

Denotes the force that follows through.”

Then m sub one hit youth on dome

And gave conviction to this pome.

86. THE PLATE OF PIE

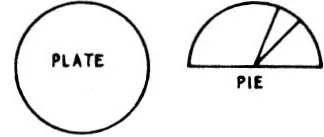
Fig. 48

Viktors Linis, Saskatchewan, wants to know the diameter of the smallest circular plate on which a semi-circular pie can be placed if the pie is cut in sectors of the same radius as the pie?

87. ROD IN THE BEAKER

M. F. Thomas, Socony Vacuum Oil Co., N. Y., contributes this one: A cylindrical iron bar, one square centimeter in cross-section, is suspended vertically over a beaker, two square centimeters in cross-section and partly filled with water, so that the bar just touches the surface of the water. The beaker stands on one pan of a balance scale; the other pan carries an empty beaker and sufficient gram weights to balance the scale. One cubic centimeter of water is added to the first beaker. How much water must be added to the other beaker to bring the scale back to balance?

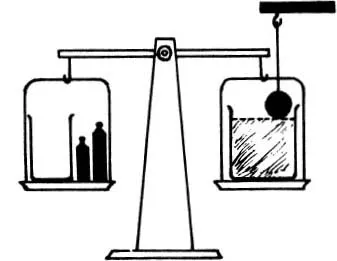
Fig. 49

88. MARKET FOR HOGS

There were three men called John, James, and Henry and their wives, Mary, Sue, and Ann, but not respectively. They went to market to buy hogs. Each person bought as many hogs as that person spent dollars per hog. John bought 23 hogs more than Sue; and James bought 11 more than Mary. Each man spent $63 more than his wife. What was the name of each man’s wife?

89. PASSING STREETCARS

A man walks at 3 mph down a street along which runs a streetcar line. He notices that, while 40 streetcars pass him traveling in the same direction as he walks, 60 pass him in the opposite direction. What is the average speed of the streetcars? In solving this one, please give adequate proof of your answer and tell how long it took you.

90. COMMON BIRTHDAYS

A. H. Phelps Jr., Cincinnati, reports that little Euclid arrived smilingly at the classroom on his birthday and after receiving the congratulations of teacher Smith and the other 29 students, remarked, “I don’t know if any other boy in the class has his birthday today but I’ll bet ten cents to four bits that there are at least two boys in the room who celebrate their birthdays on the same day, whenever that may be.” Mr. Smith, after mentally setting up the fraction 30/365 thought that Euclid was giving generous odds and that he would be sadly out of pocket if he went through the school, which had a couple dozen classrooms of that size, making such a bet. Just how foolish was our little Euclid?

91. RESISTANCE ’CROSS THE CUBE

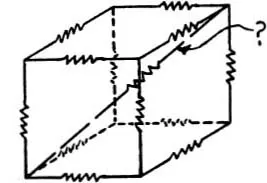
Fig. 50

A 1″ cube has its outline constructed out of wire whose resistance is one ohm per inch. What is the resistance between opposite corners of the cube?

92. MEDIANS AND OLDHAMS

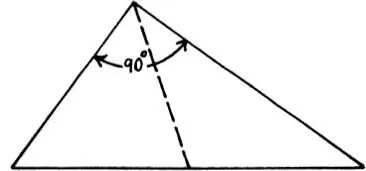
Fig. 51

What is the quickest way to prove that the median to the hypotenuse of a right triangle is equal to half the hypotenuse? And, from a practical angle, if you happen to be familiar with shaft couplings, what has this got to do with an Oldham coupling?

93. THE BACKWARD BICYCLE

Try your hand at this “experiment in mechanics” devised by Prof. Ernest Rabinowicz, M.I.T.: The pedals of an ordinary bicycle are so positioned that one is below the other and t...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Foreword
• 75 PROVOCATIVE PROBLEMS
• 25 CHALLENGING QUICKIES
• Back Cover