Circuits, Matrices and Linear Vector Spaces

Lawrence P. Huelsman

• Publisher: Dover Publications
• Year: 2013
• eBook ISBN: 9780486280448
• Topic: Technology & Engineering
• Subtopic: Engineering General
• Index: Technology & Engineering

This high-level undergraduate text explains the mathematics behind basic circuit theory. Its self-contained treatment covers matrix algebra, which provides a general means of formulating the details of a linear system. In addition, the author presents the basic theory of n-dimensional spaces and demonstrates its application to linear systems.
A development of the mathematics of matrix algebra and determinants is followed by the application of matrix techniques to a general discussion of circuits. Subsequent topics include the properties of active and passive two-port devices, the basic theory of linear vector spaces, and the natural frequencies of a network. Appendixes cover the indefinite-transfer matrix, gyrators with complex gyration admittance, and network transformations. A wealth of equations and calculation problems appear throughout the text.

Chapter 1 Introduction

1.1 Circuits and circuit elements

There are several classifications under which circuits, as they are studied today, may be grouped. Some of these classifications are determined by the properties of the circuit elements, and some of them are the result of the manner in which these elements are interconnected. In this chapter we shall present some of the basic ideas concerning the classification of circuits and circuit elements according to their properties. This material will serve to introduce some of the terms that will frequently appear in later sections of the book. It will also serve to review some of the basic ideas of circuit theory. Additional information on the topics of this chapter can be found in the references listed in the final section of the chapter.

1.2 Classifications of circuit elements

In a consideration of the elements of which a circuit is composed, a first distinction must be made as to the number of terminals that such elements possess. Since a one-terminal element is without physical significance, let us begin by considering elements with two terminals. These elements can, in general, be grouped according to the following divisions: linear or non-linear, lumped or distributed, passive or active. Let us consider each of these classifications and discuss its principal characteristics.

A linear element can be defined in terms of the requirements of superposition and homogeneity. Superposition requires that, if two inputs are simultaneously applied to an element, the result be the sum of the results obtained from separate application of those same inputs. Thus, if the result of applying a d-c voltage of 1 volt to a given element is a d-c current of 1 amp through the element, and the result of applying an a-c voltage, sin 2t, to the element is a current 2 sin 2t, superposition requires that, if an input voltage 1 + sin 2t is applied to the element, a current 1 + 2 sin 2t results. The principle of homogeneity may be explained as follows: If a given input produces a certain result, then multiplying the magnitude of the input by a constant will multiply the value of the result by the same constant. A linear circuit element is one which satisfies the requirements of superposition and homogeneity. No physical device is actually linear; however, it is convenient to approximate such devices by models which are idealized in the sense that they are defined as being linear.

A lumped element is one whose properties can be considered as concentrated in space. From another viewpoint, it is one in which the time of propagation of electrical phenomena through the element is zero. A transmission line is an example of a nonlumped element, i.e., a distributed device. Actually, all physical devices can be considered as being distributed, since they have nonzero dimensions. It is convenient, however, to approximate physical devices by models which are considered as lumped. Thus, we shall treat our circuit elements as lumped and linear.

Three of the basic circuit elements which we shall consider are the positive-valued resistor, the positive-valued inductor, and the positive-valued capacitor. These are the elements that relate voltage and current, voltage and the derivative of current, and voltage and the integral of current, respectively. They will be treated as lumped linear elements. They are considered as passive elements in that they approximate physical devices which do not require a source of energy to achieve their specified properties. We shall see that elements which can be described as negative-valued resistors, inductors, and capacitors can also be considered in our circuit studies. The physical devices which these elements approximate, in general, require external power sources to sustain their operation. Thus, these elements will be referred to as active elements.

Two other elements which we shall use in our discussion of circuits are the voltage source and the current source. These are both models which may or may not approximate physical devices, depending on the inclusion of parasitic elements of resistance, capacitance, and inductance. The voltage source has zero internal impedance, i.e., the voltage existing at its terminals is independent of the current flowing through the element. If its output voltage is a function of some other voltage or current in the circuit, it is said to be a dependent source. If it has an output which is not a function of any of the circuit variables (it may still, of course, be a function of time), it is said to be an independent source. Similarly, the current source has infinite internal impedance, i.e., its output current is independent of the potential difference existing across its terminals. It may be a dependent source, in which case its output will be a function of some other voltage or current in the circuit, or an independent source.

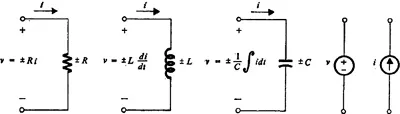
Figure 1.1 Symbols for circuit elements.

The usual symbols for the lumped linear passive and active circuit elements discussed above are shown in Fig. 1.1. In addition to these two-terminal elements, there are also some fundamental three-terminal and four-terminal circuit elements. These are the ideal transformer, the negative-immittance converter, and the gyrator. These are all linear elements. A more detailed discussion of them will be given in Chap. 4.

1.3 Classifications of circuits

Classifications similar to those made for the circuit elements described in the preceding section can be made for circuits comprised of such elements. There are, however, some interesting special cases. For example, we can consider a linear circuit as one comprised of linear elements, and thus we expect that the requirements of superposition and homogeneity will apply. An exception occurs when independent sources are present in the network. For example, consider the network shown in Fig. 1.2. If a voltage v of 5 volts is applied to this circuit, the current i is zero. Similarly, if a voltage v of 10 volts is applied, the current i is 1 amp. However, a voltage of 15 volts, which represents the simultaneous application of both the above inputs, causes a current of 2 amps to flow, in clear violation of the properties of linearity. Despite such discrepancies, it is convenient, in a broad sense, to consider as linear circuits those which are comprised of linear elements. It is easy to see that the usual techniques of linear circuits are adequate to treat such cases. In general, circuits which contain linear elements and dependent sources satisfy the definition of linearity.

Figure 1.2 A circuit with an independent source.

In a similar fashion, special cases may occur when we seek to define the criteria under which a circuit may be considered as active or passive. For example, the series connection of a positive-valued 3-ohm resistor and a negative-valued 1-ohm resistor will act as a positive-valued 2-ohm resistor. Thus we see that a circuit which contains active (in this case negative-valued) elements, can still act as a passive circuit. Despite this, however, it is convenient to define an active circuit as one which contains at least one active element. This definition will be used in the chapters that follow.

A classification that is made for circuits but which is not applicable to circuit elements is the division into reciprocal and nonreciprocal circuits. If, in a given circuit, when the points of excitation and observation of response are interchanged, the relationship between these two quantities remains the same, the circuit is said to be reciprocal. The interchange must not, of course, change the network. For a given circuit to be reciprocal, the above property must be true for any choice of the points of excitation and observation of response. A further discussion of the properties of reciprocal networks is given in Chap. 3. We shall point out at this time, however, that circuits composed entirely of linear R, L, and C elements, both negative- and positive-valued, are always reciprocal. Circuits which contain dependent sources may or may not be reciprocal. Nonreciprocal circuits usually fall into two categories. First, they may be unilateral, in the sense that when some points of excitation and observation of response are interchanged, no response is observed. Second, they may provide different relations between excitation and response when these quantities are interchanged. As examples, consider th...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication
• Preface
• Contents
• Chapter 1 Introduction
• Chapter 2 Matrices and determinants
• Chapter 3 Circuit-theory applications of matrices
• Chapter 4 Two-port devices
• Chapter 5 Linear vector spaces
• Chapter 6 Circuit-theory applications of linear vector spaces
• Appendix A The indefinite-transfer matrix
• Appendix B Gyrators and gyration admittance
• Appendix C Network realization by transformation methods
• Index
• Back Cover