An Introduction to the Theory of Groups

Paul Alexandroff, Hazel Perfect, Hazel Perfect, G.M. Petersen

• Publisher: Dover Publications
• Year: 2013
• eBook ISBN: 9780486275970
• Topic: Mathematics
• Subtopic: Group Theory
• Index: Mathematics

This introductory exposition of group theory by an eminent Russian mathematician is particularly suited to undergraduates, developing material of fundamental importance in a clear and rigorous fashion. The treatment is also useful as a review for more advanced students with some background in group theory.
Beginning with introductory examples of the group concept, the text advances to considerations of groups of permutations, isomorphism, cyclic subgroups, simple groups of movements, invariant subgroups, and partitioning of groups. An appendix provides elementary concepts from set theory. A wealth of simple examples, primarily geometrical, illustrate the primary concepts. Exercises at the end of each chapter provide additional reinforcement.

Chapter I

THE GROUP CONCEPT

§ 1. Introductory examples

1. Operations with whole numbers

The addition of whole numbers * satisfies the following conditions, which we call axioms of addition and which are of very great importance for all that follows:

I. Two numbers can be added together (i.e. to any two arbitrary numbers a and b there corresponds a uniquely determined number, which we call their sum: a + b).

II. The Associative Law:

For any three arbitrary numbers a, b, c we have the following identity

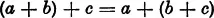
III. Among the numbers there is a uniquely determined number 0, the zero, which is such that for every number a the relation

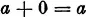
is satisfied.

IV. To every number a there corresponds a so-called inverse (or negative) number —a, which has the property that the sum a + (—a) is equal to zero:

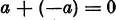
Finally yet another important condition is satisfied.

V. The Commutative Law:

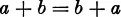
2. The rotations of an equilateral triangle

We show that it is possible to add not only numbers but also many other kinds of things, and that the above conditions remain satisfied.

First Example.—We consider all possible rotations of an equilateral triangle ABC about its centroid 0 (fig. 1). We agree to call two rotations identical if they only differ from one another by a whole number of complete revolutions (and therefore by an integral multiple of 360°*). We see without difficulty that of all possible rotations of the triangle only three rotations send it into coincidence with itself, namely, the rotations through 120°, 240°, and the so-called zero rotation, which leaves all the vertices unchanged and hence also all the sides of the triangle. The first rotation sends the vertex A into the vertex B, the vertex B into the vertex C, the vertex C into the vertex A (we say that it permutes cyclically the vertices A, B, C). The second rotation sends A into C, B into A, C into B, and therefore permutes A,C,B cyclically.

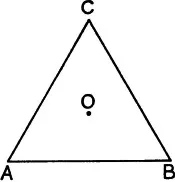
Fig. 1

Now we introduce the following natural definition: The addition of two rotations means their successive application, the first rotation followed by the second. If we add the rotation through 120° to itself, then the result is the rotation through 240°; if we add to it the rotation through 240°, then the result is the rotation through 360°, the zero rotation. Two rotations through 240° result in the rotation through 480° = 360° + 120°; their sum is therefore the rotation through 120°. If we denote the zero rotation by a₀, the rotation through 120° by a₁, the rotation through 240° by a₂, then we obtain the following relations:

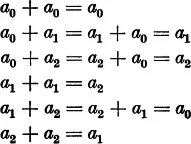
Thus the sum of any two of the rotations a₀, a₁, a₂ is defined and is again one of the rotations a₀, a₁, a₂ We easily convince ourselves that this addition satisfies the associative law and evidently also the commutative law. Further, there exists among these rotations a₀, a₁, a₂ a zero rotation a₀ which satisfies the...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Translators’ Foreword
• from the Foreword to the First Edition
• Contents
• CHAPTER ONE. THE GROUP CONCEPT
• CHAPTER TWO. GROUPS OF PERMUTATIONS
• CHAPTER THREE. SOME GENERAL REMARKS ABOUT GROUPS. THE CONCEPT OF ISOMORPHISM
• CHAPTER FOUR. CYCLIC SUBGROUPS OF A GIVEN GROUP
• CHAPTER FIVE. SIMPLE GROUPS OF MOVEMENTS
• CHAPTER SIX. INVARIANT SUBGROUPS
• CHAPTER SEVEN. HOMOMORPHIC MAPPINGS
• CHAPTER EIGHT. PARTITIONING OF A GROUP RELATIVE TO A GIVEN SUBGROUP. DIFFERENCE MODULES
• APPENDIX. ELEMENTARY CONCEPTS FROM THE THEORY OF SETS
• BOOKS TO CONSULT
• INDEX
• Back Cover