Logic in Elementary Mathematics

Robert M. Exner, Myron F. Rosskopf

• Publisher: Dover Publications
• Year: 2011
• ISBN:
  9780486264226
• Topic: Mathematics
• Subtopic: Logic in Mathematics
• Index: Mathematics

This applications-related introductory treatment explores facets of modern symbolic logic useful in the exposition of elementary mathematics. The authors convey the material in a manner accessible to those trained in standard elementary mathematics but lacking any formal background in logic.
Topics include the statement calculus, proof and demonstration, abstract mathematical systems, and the restricted predicate calculus. The final chapter draws upon the methods of logical reasoning covered in previous chapters to develop solutions of linear and quadratic equations, definitions of order and absolute value, and other applications. Numerous examples and exercises aid in the mastery of the language of logic.

V:	THE RESTRICTED PREDICATE CALCULUS

5.1 STATEMENT FUNCTIONS

Our treatment of formal logic up to this point has been limited to consideration of statements, relations between statements, and arguments that can be expressed as sequences of statements. The symbols “A”, “B”, … were always interpreted as translations of whole statements. It was possible to consider some complex statements as compounds of simpler statements, and to express the complex structure symbolically by means of the connectives “&”, “∨”, etc. The machinery so far developed is not yet adequate to reflect all the formal aspects of mathematical arguments. For instance, in the long demonstration of (3.34) the axioms A₁, A₂, A₃, A₄ as written are statements about three natural numbers whose names are “x”, “y”, and “z”, but are treated as statements about any three natural numbers. We shall examine this procedure more closely in the succeeding sections. Also, the long demonstration was a proof of

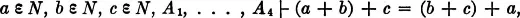
but a theorem about natural numbers ought to be a statement about natural numbers that follows from the axioms, and not from the axioms and some additional ad hoc assumptions. We should have liked to deduce from the axioms alone some such statement as

For all natural numbers a, b, c, (a + b) + c = (b + c) + a,

but the formal machinery for doing so was lacking. To develop the formal machinery, it will be necessary to examine more closely Steps 3 and 6 of the pattern of conventional proofs given in Sec. 3.12. Step 3 is concerned with stating a geometric theorem in terms of particular, though unknown, points and lines, and Step 6 is concerned with the ultimate generalization from a statement about particular points and lines to a statement about all points and lines.

In the introduction, the Socrates Argument was presented as an example of a formal argument:

All men are mortal.

Socrates is a man.

∴ Socrates is mortal.

In Sec. 2.1 it was asserted that the statement calculus is not adequate to handle such an argument because its validity depends on subject and predicate relations. We could, of course, translate the three statements, respectively, “A”, “B”, “C”, and symbolize the argument

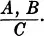
But we have no inference rules to apply here to infer “C” from “A” and “B”, and so have no formal way of checking the validity of the argument.

To develop the necessary formalism, let us begin by considering the simpler of the two premises, namely,

(5.1) Socrates is a man.

The statement asserts that the individual Socrates has the property of being human (or being a man, or being a member of the class men). The name “Socrates” designates the individual who has the property, and the predicate “is a man” indicates the property. We choose “H( )” as a symbolic translation of the predicate “is a man”, and may then translate (5.1)

H(Socrates).

More neatly, we may take “s” as another name for Socrates, and translate (5.1)

(5.2) H(s).

The symbol “H(s)” consists of two parts, the predicate symbol “H( )” and the individual symbol “s”. Statements similar to (5.1) could be translated in a similar way:

H(e): The Eiffel tower is a man.

(5.3) H(j): Joe is...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Glossary of Special Symbols and Abbreviations
• I. Mathematics, Formal Logic, and Names
• II. The Statement Calculus
• III. Proof and Demonstration
• IV. Abstract Mathematical Systems
• V. The Restricted Predicate Calculus
• VI. Applications of Logic in Mathematics
• Appendix. Symbolic Treatment of the Miniature Geometry
• Index
• Back Cover