A Short Course in Automorphic Functions

Joseph Lehner

• Publisher: Dover Publications
• Year: 2014
• Print ISBN: 9780486789743
• eBook ISBN: 9780486799926
• Topic: Mathematics
• Subtopic: Complex Analysis
• Index: Mathematics

This concise three-part treatment introduces undergraduate and graduate students to the theory of automorphic functions and discontinuous groups. Author Joseph Lehner begins by elaborating on the theory of discontinuous groups by the classical method of Poincaré, employing the model of the hyperbolic plane. The necessary hyperbolic geometry is developed in the text. Chapter two develops automorphic functions and forms via the Poincaré series. Formulas for divisors of a function and form are proved and their consequences analyzed. The final chapter is devoted to the connection between automorphic function theory and Riemann surface theory, concluding with some applications of Riemann-Roch theorem.
The book presupposes only the usual first courses in complex analysis, topology, and algebra. Exercises range from routine verifications to significant theorems. Notes at the end of each chapter describe further results and extensions, and a glossary offers definitions of terms.

[ I ]

Discontinuous Groups

An analytic function f is called automorphic with respect to a group Γ of transformations of the plane if f takes the same value at points that are equivalent under Γ. That is,

for each V ∈ Γ and each z ∈ D, the domain of f. If we want to have nonconstant functions f, we must assume there are only finitely many equivalents of z lying in any compact part of D. This property of Γ is known as discontinuity.

The most important domain for f from the standpoint of applications is the upper half-plane ^† H. Now from (1) with f analytic in H we deduce that V is analytic in H and maps H into itself. It is natural to require that V be one-to-one in order that V⁻¹ should be single-valued. Hence F is a linear-fractional transformation. The group Γ will therefore be a group of linear-fractional transformations, or as we shall call them, linear transformations.

The present chapter is devoted to a study of discontinuous groups of linear transformations.

1. Linear Transformations

1A. A linear transformation is a nonconstant rational function of degree 1; that is, a function

where α, β, γ, δ are complex numbers and z is a complex variable. The function w is defined on all of the complex sphere Z except z = −δ/γ and z = ∞. With the usual convention that w/0 = ∞ for u ≠ 0, we have

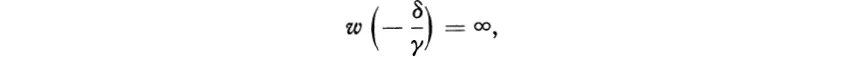
and we obtain w(∞) by continuity:

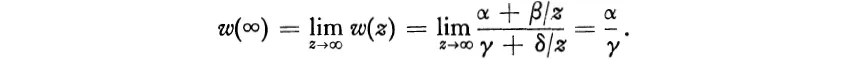
In particular, −δ/γ will be ∞ if and only if γ = 0, and in that case α/γ = ∞: the infinite points of the two planes then correspond under the mapping w.

As a rational function, w is regular in Z except for a simple pole at z = −δ/γ. Suppose γ = 0. Then necessarily δ ≠ 0, α ≠ 0 (because of αδ − βγ ≠ 0) and

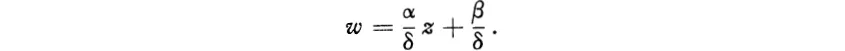
Hence dw/dz = α/δ ≠ 0 and w is conformal at every finite z. At infinity we must use the uniformizing variables z′ = l/z, w′ = 1/w; then we find that

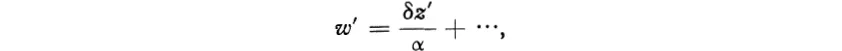
and w′ is conformal at z′ = 0, which by definition means that w is conformal at z = ∞.

If γ ≠ 0, we have

hence dw/dz ≠ 0 and w is conformal except possibly at z = −δ/γ, z = ∞. At z = − δ/γ we must use the variables z′ = z + δ/γ, w′ = 1/w:

so that (dw′/dz′)_{z = 0} ≠ 0. At z = ∞ the correct variables are z′ = 1/z, w′ = w and we get

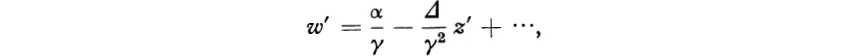
yielding the same conclusion.

Solving (2) for z we get

which is also a linear transformation and so is defined on the extended w-plane. The mapping z → w is therefore onto and hence one-to-one, and we may write z = w⁻¹.

Putting these results together we can assert:

THEOREM. The linear transformation (2) is a one-to-one conformal mapping of all of Zon itself.

For this reason a linear transformation is also called a con...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Preface
• Chapter I. Discontinuous Groups
• Chapter II. Automorphic Functions and Automorphic Forms
• Chapter III. Riemann Surfaces
• References
• Glossary
• Index