A Book of Set Theory

Charles C Pinter

• Publisher: Dover Publications
• Year: 2014
• Print ISBN: 9780486497082
• eBook ISBN: 9780486795492
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

Suitable for upper-level undergraduates, this accessible approach to set theory poses rigorous but simple arguments. Each definition is accompanied by commentary that motivates and explains new concepts. Starting with a repetition of the familiar arguments of elementary set theory, the level of abstract thinking gradually rises for a progressive increase in complexity.
A historical introduction presents a brief account of the growth of set theory, with special emphasis on problems that led to the development of the various systems of axiomatic set theory. Subsequent chapters explore classes and sets, functions, relations, partially ordered classes, and the axiom of choice. Other subjects include natural and cardinal numbers, finite and infinite sets, the arithmetic of ordinal numbers, transfinite recursion, and selected topics in the theory of ordinals and cardinals. This updated edition features new material by author Charles C. Pinter.

1

Classes and Sets

1 BUILDING SENTENCES

Before introducing the basic notions of set theory, it will be useful to make certain observations on the use of language.

By a sentence we will mean a statement which, in a given context, is unambiguously either true or false. Thus

London is the capital of England.

Money grows on trees.

Snow is black.

are examples of sentences. We will use letters P, Q, R, S, etc., to denote sentences; used in this sense, P, for instance, is to be understood as asserting that “P is true.”

Sentences may be combined in various ways to form more complicated sentences. Often, the truth or falsity of the compound sentence is completely determined by the truth or falsity of its component parts. Thus, if P is a sentence, one of the simplest sentences we may form from P is the negation of P, denoted by ¬P (to be read “not P ”), which is understood to assert that “P is false.” Now if P is true, then, quite clearly, ¬P is false; and if P is false, then ¬P is true. It is convenient to display the relationship between ¬P and P in the following truth table,

where t and f denote the “truth values”, true and false.

Another simple operation on sentences is conjunction: if P and Q are sentences, the conjunction of P and Q, denoted by P ∧ Q (to be read “P and Q”), is understood to assert that “P is true and Q is true.” It is intuitively clear that P ∧ Q is true if P and Q are both true, and false otherwise; thus, we have the following truth table.

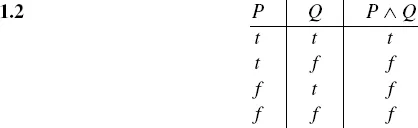
The disjunction of P and Q, denoted by P ∨ Q (to be read “P or Q”), is the sentence which asserts that “P is true, or Q is true, or P and Q are both true.” It is clear that P ∨ Q is false only if P and Q are both false.

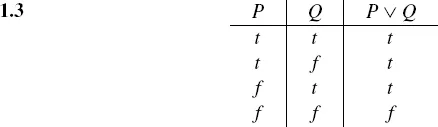
An especially important operation on sentences is implication : if P and Q are sentences, then P ⇒ Q (to be read “P implies Q”) asserts that “if P is true, then Q is true.” A word of caution: in ordinary usage, “if P is true, then Q is true” is understood to mean that there is a causal relationship between P and Q (as in “if John passes the course, then John can graduate”). In mathematics, however, implication is always understood in the formal sense: P ⇒ Q is true except if P is true and Q is false. In other words, P ⇒ Q is defined by ...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Contents
• Preface
• Chapter 0 Historical Introduction
• Chapter 1 Classes and Sets
• Chapter 2 Functions
• Chapter 3 Relations
• Chapter 4 Partially Ordered Classes
• Chapter 5 The Axiom of Choice and Related Principles
• Chapter 6 The Natural Numbers
• Chapter 7 Finite and Infinite Sets
• Chapter 8 Arithmetic of Cardinal Numbers
• Chapter 9 Arithmetic of the Ordinal Numbers
• Chapter 10 Transfinite Recursion. Selected Topics in the Theory of Ordinals
• Chapter 11 Consistency and Independence in Set Theory
• Bibliography
• Index