Linear Programming: An Introduction to Finite Improvement Algorithms

Second Edition

Daniel Solow

• Publisher: Dover Publications
• Year: 2014
• ISBN:
  9780486782171
• Edition: 2
• Topic: Mathematics
• Subtopic: Linear & Nonlinear Programming
• Index: Mathematics

Suitable for undergraduate students of mathematics and graduate students of operations research and engineering, this text covers the basic theory and computation for a first course in linear programming. In addition to substantial material on mathematical proof techniques and sophisticated computation methods, the treatment features numerous examples and exercises.
An introductory chapter offers a systematic and organized approach to problem formulation. Subsequent chapters explore geometric motivation, proof techniques, linear algebra and algebraic steps related to the simplex algorithm, standard phase 1 problems, and computational implementation of the simplex algorithm. Additional topics include duality theory, issues of sensitivity and parametric analysis, techniques for handling bound constraints, and network flow problems. Helpful appendixes conclude the text, including a new addition that explains how to use Excel to solve linear programming problems.

Chapter 1

Problem Formulation

The success and survival of any organization depend on the quality of the decisions made by its managers. The central issue in many problems arising in business, industry, and government is that various activities compete for limited resources. It is the responsibility of the decision maker to allocate the resources among the competing activities so as to achieve the best results for the organization. The decision maker needs tools and techniques that can help in the quest for the optimal allocation of resources. Linear programming is the study of a large and important class of these problems together with the procedures currently available for obtaining their solutions. In this chapter, you will learn what a linear programming problem is, how to identify and to formulate one, and what distinguishes it from other types of problems.

1.1. WHAT IS A LINEAR PROGRAMMING PROBLEM?

To understand what a linear programming problem is, consider the dilemma of Midas M. Miner. One day he was traveling through the galaxy in his luxury spaceship when he developed minor engine trouble and was forced to land on a nearby asteroid. After making the necessary repairs, he was astounded (and delighted) to discover that the asteroid contained large quantities of silver ore and gold ore. Naturally, Midas wanted to take the whole asteroid with him, but practical considerations dictated otherwise. He knew that his ship could carry up to 100 pounds of extra cargo as long as it did not take up more than 150 cubic feet of space. After some measurements, Midas calculated that each pound of gold ore requires 2 cubic feet but each pound of silver ore requires only 1 cubic foot. Given that each pound of gold ore is worth 3 intergalactic credits (each credit being equivalent to approximately $10,000) and each pound of silver ore is worth 2 credits, how many pounds of each type of ore should Midas put on his ship so as to maximize his profit and still be able to take off?

In this problem, it is necessary to determine the quantities of gold and silver ore that Midas should take so as to achieve the maximum possible profit. Since it is not known in advance what these quantities should be, let x₁ and x₂ represent the number of pounds, respectively, of each of the two ores to be loaded on the ship. The variables x₁ and x₂ are sometimes called decision variables.

Since each pound of gold ore is worth 3 intergalactic credits, the worth of x₁ pounds of gold ore would be 3x₁ credits. Similarly, the worth of x₂ pounds of silver ore would be 2x₂ credits since each pound is worth 2 credits. Therefore, Mr. Miner’s total profit would be 3x₁ + 2x₂ credits. The function 3x₁ + 2x₂ is called the objective function because the objective of the problem is to find values for x₁ and x₂ that maximize this function. Suppose, for instance, that x₁ and x₂ are chosen to be 40 pounds and 50 pounds, respectively. The corresponding profit would be 3(40) + 2(50) = 220 credits. On the other hand, if x₁ is 60 pounds and x₂ is 80 pounds, then the total profit would be 3(60) + 2(80) = 340 credits. Evidently, as x₁ and x₂ are increased, so are the profits. What is it, then, that prevents Midas from making an infinite profit? Evidently, it is the limited capacity of his cargo space.

If Midas decides to take x_l pounds of gold ore and x₂ pounds of silver ore, then the total weight of the cargo will be x₁ + x₂ pounds. Similarly, since each pound of gold ore requires 2 cubic feet of space and each pound of silver ore requires 1 cubic foot, the total volume of the cargo will be 2x_l + x₂ cubic feet. For the specific case in which x₁ and x₂ are chosen to be 40 and 50 pounds, respectively, the corresponding total weight of the cargo would be x₁ + x₂ = 40 + 50 = 90 pounds, and the volume of this cargo would be 2x₁ + x₂ = 2(40) + (50) = 130 cubic feet. Since the ship can indeed hold 100 pounds and 150 cubic feet of cargo, Mr. Miner will have no trouble taking off with 40 pounds of gold ore and 50 pounds of silver ore. For this reason, the choice of x₁ = 40, x₂ = 50 is said to be feasible.

In contrast, consider the case in which x_l is 60 and x₂ is 80. The weight and volume of the resulting cargo are 140 pounds and 200 cubic feet, respectively. Since these quantities exceed the ship’s capacity, it is not possible to take 60 pounds of gold ore and 80 pounds of silver ore aboard the ship. For this reason, the choice x₁ = 60, x₂ = 80 is said to be infeasible.

The conclusion is that Midas is constrained by the limited cargo capacity, and so his profits are limited also. The constraint on the total weight of the cargo can be expressed mathematically by the inequality

x₁ + x₂ ≤ 100

Similarly, the total volume of the cargo should be less than or equal to 150 cubic feet, so

2x₁ + x₂ ≤ 150

These are two constraints that x₁ and x₂ should satisfy, but are there any other restrictions on the variables? Although there are none explicitly stated in the problem, there is an implied understanding that the values of x₁ and x₂ should be ≥ 0 because it is not possible to have negative quantities of rocks. These implicit nonnegativity constraints can be made explicit by writing the inequalities

x₁ ≥ 0, x₂ ≥ 0

Such constraints should be included in the formulation of any real world problem whenever appropriate.

In mathematical terms, Mr. Miner’s problem can be stated as follows:

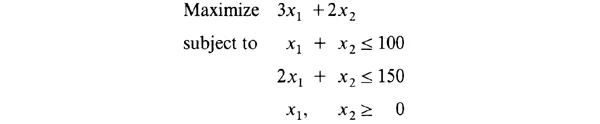
The above problem is a linear programming problem (hereafter referred to as an LP). I...