Mathematical Techniques for Biology and Medicine

William Simon

• Publisher: Dover Publications
• Year: 2015
• eBook ISBN: 9780486780795
• Edition: 4
• Topic: Biological Sciences
• Subtopic: Biology
• Index: Biological Sciences

This pioneering book was one of the first to describe the use of advanced mathematical methods in the life sciences. Used widely in one-semester courses, it assumes only elementary calculus and proceeds rapidly, but in a complete and self-contained way, through techniques essential to medicine and biology. Some techniques are unique to this volume and others emphasize the chemical and physical principles underlying biological processes. Less emphasis is given to formal solutions than to methods designed to develop physical intuition and to numerical solutions.
Full chapters are devoted to compartmental problems, regulation and oscillation of feedback control systems, numerical methods, diffusion processes, blood flow measurements, curve fitting, and the use of tracers. Unlike most mathematical texts, this book avoids engineering terminology since it is often unfamiliar to biologists. A problem section is included at the end of each chapter, with problems ranging from relatively simple to fairly challenging. Fully worked-out solutions are included for some of the problems.
This new fourth edition includes an updated preface and an appendix with sample programs.

VII

Regulation and Oscillation

1. The Sine and Cosine Functions

In elementary trigonometry the sine and cosine functions are initially defined in terms of the two angles of the right triangle that are less than 90°. The sine of the angle is the length of the side opposite the angle divided by the length of the hypotenuse, while the cosine of the angle is the length of the side adjacent to the angle divided by the length of the hypotenuse (Figure 7-1). These definitions are then extended to angles between 90° and 180° by defining the adjacent side in the negative direction from the origin, and to negative angles by defining the opposite side as being negative in the downward direction, as in Figure 7-2. They are still further extended to angles greater than plus or minus 180° by adding or subtracting multiples of the angle corresponding to a full circle, 360°. Thus, we have the following rules.

Rule: If 90° < θ < 180°, then

sin θ = sin(180° - θ)

cos θ = -cos(180°- θ)

Rule: For negative angles,

sin - θ= -sin(+θ)

cos - θ = cos(+θ)

There is one important difference between the way in which the sine and cosine functions are used in elementary trigonometry and the way in which they are used in calculus: in calculus, angles are almost always defined in terms of radians rather than degrees, with 2π radians being a full circle. The

Figure 7-1. Definitions of the sine of an angle and the cosine of an angle in terms of the sides of a right triangle for angles less than and greater than 90°.

Figure 7-2. Definition of a sine of an angle and the cosine of an angle in terms of negative angles.

reason for this has to do with their derivatives. If the angles are defined in terms of radians, the derivatives of sine and cosine are given by

and by the chain rule

These derivatives are derived in Appendix III.

In Figure 7-3 we have plotted the values of the sine and cosine of an angle θ from θ equal to – 3π radians to + 3π radians.

Figure 7-3. Plots of the sine and cosine functions as functions of angles shown as solid lines. The sine of five times the angle and the cosine of twice the angle are shown as dotted lines.

The importance of the sine and cosine functions in this book lies not in their geometrical interpretation but rather in the fact that they are solutions to an important class of differential equations. If

and

the solution is

which we verify by using Eqs. (7.3) and (7.4)

Similarly, if

and

the solution is

which we leave for the reader to verify.

We can now find the Laplace transforms of the sine and cosine functions by taking advantage of the fact that we know the differential equations to which they are solutions. (More precisely, we know one such differential equation for each.) We could presumably find their Laplace transform from the definition of the transform given in Chapter 4, but the integrals are difficult to evaluate. Let us therefore take the Laplace transform of Eq. (7.5) with its accessory conditions (7.6),

solve for g, and since we know that the inverse of g is the sine function, we have

We leave as an exercise the derivation, using the same method, of the Laplace transform of the cosine, which is

In this chapter we shall encounter a second-order differential equation whose solution for certain values of the constants is approximately a simple decaying exponential, while for other values of the constants the solution varies sinusoidally with time. It seems plausible, then, that for the intermediate values of the constants the solutions will be a compromise between these two extremes. Let us therefore examine functions of the type

to see what kinds of differential equations they satisfy, and by means of these establish the Laplace transform of f₁ and f₂. We begin with f₁, which we differentiate twice.

Let us attempt to construct a simple different...

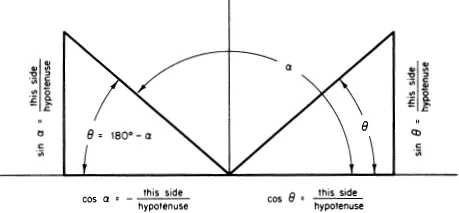
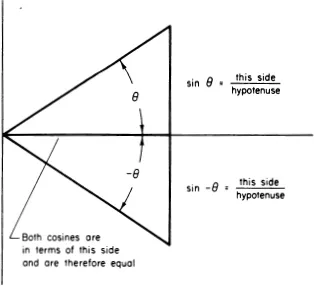
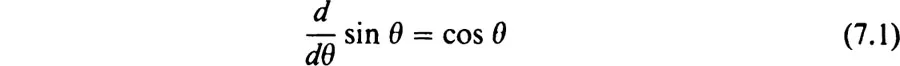
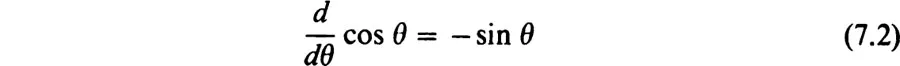
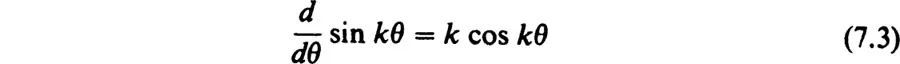
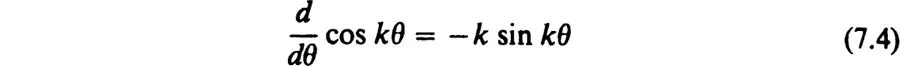
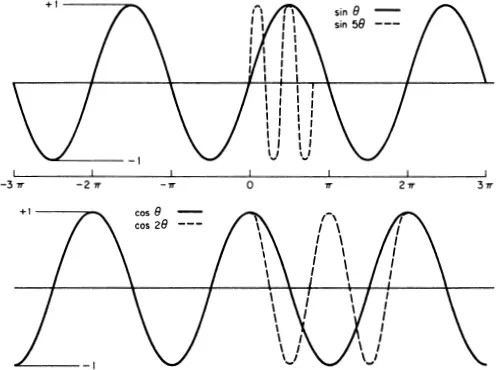
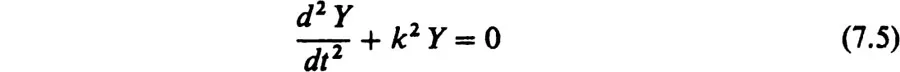
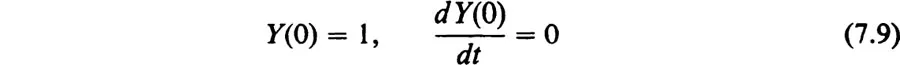
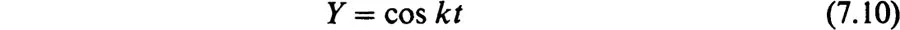
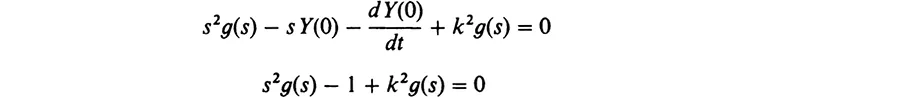
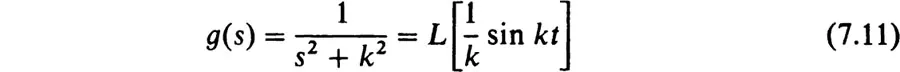
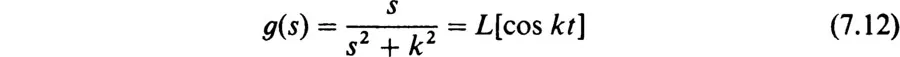
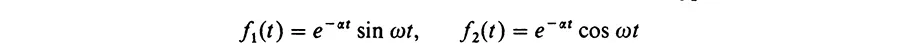
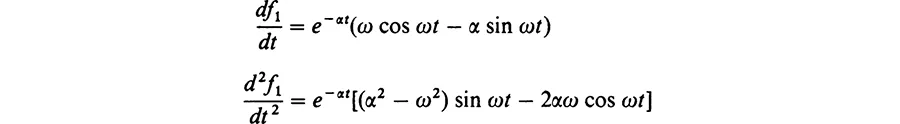
Table of contents

• Cover
• Title Page
• Copyright Page
• Table of Contents
• Preface to the Fourth Edition
• Preface
• Review of Differential Calculus
• II. How Differential Equations Arise
• III. Guessing the Solution of a Differential Equation
• IV. The Laplace Transform
• V. Compartmental Problems
• VI. Numerical Methods
• VII. Regulation and Oscillation
• VIII. Diffusion
• IX. The Theory of Blood Flow Measurement
• X. Curve Fitting
• XI. Tracer Experiments
• Appendix I. The Derivative of the Exponential Function
• Appendix II. Table of Laplace Transforms
• Appendix III. Derivatives of Sine and Cosine Functions
• Appendix IV. Solutions to Selected Problems
• Appendix V. Additional Problems
• Appendix VI. Solutions to Additional Problems
• Appendix VII. Sample Programs
• References
• Index