536 Puzzles and Curious Problems

Henry E. Dudeney, Martin Gardner

• Publisher: Dover Publications
• Year: 2016
• Print ISBN: 9780486796864
• eBook ISBN: 9780486816104
• Edition: 1
• Topic: Mathematics
• Subtopic: Games in Mathematics
• Index: Mathematics

For two decades, self-taught mathematician Henry E. Dudeney wrote a puzzle page, "Perplexities," for The Strand Magazine. Martin Gardner, longtime editor of Scientific American's mathematical games column, hailed Dudeney as "England's greatest maker of puzzles," unsurpassed in the quantity and quality of his inventions. This compilation of Dudeney's long-inaccessible challenges attests to the puzzle-maker's gift for creating witty and compelling conundrums.
This treasury of intriguing puzzles begins with a selection of arithmetical and algebraical problems, including challenges involving money, time, speed, and distance. Geometrical problems follow, along with combinatorial and topological problems that feature magic squares and stars, route and network puzzles, and map coloring puzzles. The collection concludes with a series of game, domino, match, and unclassified puzzles. Solutions for all 536 problems are included, and charming drawings enliven the book.

Answers

Answers

1. CONCERNING A CHECK

The amount must have been $31.63. He received $63.31. After he had spent a nickel there would remain the sum of $63.26, which is twice the amount of the check.

2. DOLLARS AND CENTS

The man must have entered the store with $99.98 in his pocket

3. LOOSE CASH

The largest sum is $1.19, composed of a half dollar, quarter, four dimes, and four pennies.

4. GENEROUS GIFTS

At first there were twenty persons, and each received $6.00. Then fifteen persons (five fewer) would have received $8.00 each. But twenty-four (four more) appeared and only received $5.00 each. The amount distributed weekly was thus $120.00.

5. BUYING BUNS

There must have been three boys and three girls, each of whom received two buns at three for a penny and one bun at two for a penny, the cost of which would be exactly 7¢.

6. UNREWARDED LABOR

Weary Willie must have worked 16⅔ days and idled 13⅓ days. Thus the former time, at $8.00 a day, amounts to exactly the same as the latter at $10.00 a day.

7. THE PERPLEXED BANKER

The contents of the ten bags (in dollar bills) should be as follows: $1, 2, 4, 8, 16, 32, 64, 128, 256, 489. The first nine numbers are in geometrical progression, and their sum, deducted from 1,000, gives the contents of the tenth bag.

8. A WEIRD GAME

The seven men, A, B, C, D, E, F, and G, had respectively in their pockets before play the following sums: $4.49, $2.25, $1.13, 57¢, 29¢, 15¢, and 8¢. The answer may be found by laboriously working backwards, but a simpler method is as follows: 7 + 1 = 8; 2 × 7 + 1 = 15; 4 × 7 + 1 = 29; and so on, where the multiplier increases in powers of 2, that is, 2, 4, 8, 16, 32, and 64.

9. DIGGING A DITCH

A. should receive one-third of two dollars, and B. two-thirds. Say B. can dig all in 2 hours and shovel all in 4 hours; then A. can dig all in 4 hours and shovel all in 8 hours. That is, their ratio of digging is as 2 to 4 and their ratio of shovelling as 4 to 8 (the same ratio), and A. can dig in the same time that B. can shovel (4 hours), while B. can dig in a quarter of the time that A. can shovel. Any other figures will do that fill these conditions and give two similar ratios for their working ability. Therefore, A. takes one-third and B. twice as much—two-thirds.

10. NAME THEIR WIVES

As it is evident that Catherine, Jane, and Mary received respectively $122.00, $132.00, and $142.00, making together the $396.00 left to the three wives, if John Smith receives as much as his wife Catherine, $122.00; Henry Snooks half as much again as his wife Jane, $198.00; and Tom Crowe twice as much as his wife Mary, $284.00, we have correctly paired these married couples and exactly accounted for the $1,000.00.

11. MARKET TRANSACTIONS

The man bought 19 cows for $950.00,1 sheep for $10.00, and 80 rabbits for $40.00, making together 100 animals at a cost of $1,000.00.

A purely arithmetical solution is not difficult by a method of averages, the average cost per animal being the same as the cost of a sheep.

By algebra we proceed as follows, working in dollars: Since x + y + z = 100, then ½x + ½y + ½z = 50.

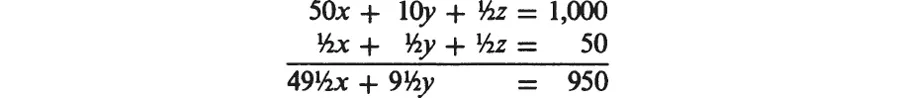
by subtraction, or 99x + 19y = 1900. We have therefore to solve this indeterminate equation. The only answer is x = 19, y = 1. Then, to make up the 100 animals, z must equal 80.

12. THE SEVEN APPLEWOMEN

Each woman sold her apples at seven for 1¢, and 3¢ each for the odd ones over. Thus, each received the same amount, 20¢. Without questioning the ingenuity of the thing, I have always thought the solution unsatisfactory, because really indeterminate, even if we admit that such an eccentric way of selling may be fairly termed a “price.” It would seem just as fair if they sold them at different rates and afterwards divided the money; or sold at a single rate with different discounts allowed; or sold different kinds of apples at different values; or sold the same rate per basketful; or sold by weight, the apples being of different sizes; or sold by rates diminishing with the age of the apples; and so on. That is why I have never held a high opinion of this old puzzle.

In a general way, we can say that n women, possessing an + (n − 1), n(a + b) + (n − 2), n(a + 2b) + (n − 3), …, n[a + b(n − 1)] apples respectively, can sell at n for a penny and b pennies for each odd one over and each receive a + b(n − 1) pennies. In the case of our puzzle a = 2, b = 3, and n − 7.

13. A LEGACY PUZZLE

The legacy to the first son was $55.00, to the second son $275.00, to the third son $385.00, and to the hospital $605.00, making $1,320.00 in all.

14. PUZZLING LEGACIES

The answer is $1,464.00—a little less than $1,500.00. The legacies, in order, were $1,296.00, $72.00, $38.00, $34.00, and $18.00. The lawyer’s fee would be $6.00.

15. DIVIDING THE LEGACY

The two legacies were $24.00 and $76.00, for if 8 (one-third of 24) be taken from 19 (one-fourth of 76) the remainder will be 11.

16. A NEW PARTNER

We must take it for granted that the sum Rogers paid, $2,500.00, was one-third of the value of the business, which was consequently worth $7,500.00 before he entered. Smugg’s interest in the business had therefore been $4,500.00 (1½ times as much as Williamson), and Williamson’s $3,000.00. As each is now to have an equal interest, Smugg will receive $2,000.00 of Rogers’s contribution, and Williamson $500.00.

17. POCKET MONEY

When he left home Tompkins must have had $2.10 in his pocket.

18. DISTRIBUTION

The smallest number original...

Table of contents

• Cover
• Title page
• Copyright
• Contents
• Introduction
• Arithmetical and Algebraical Problems
• Geometrical Problems
• Combinatorial and Topological Problems
• Game Puzzles
• Domino Puzzles
• Match Puzzles
• Unclassified Puzzles
• Answers
• Index