Weiter denken - über Philosophie, Wissenschaft und Religion

Gregor Betz, Dirk Koppelberg, David Löwenstein, Anna Wehofsits

• Publisher: De Gruyter
• Year: 2015
• eBook ISBN: 9783110382495
• Edition: 1
• Topic: Philosophy
• Subtopic: Logic in Philosophy

Philosophisches Argumentieren

dp n="90" folio="70" ? dp n="91" folio="71" ?

Ansgar Beckermann (Universität Bielefeld)

Methoden der Philosophie –gibt es rationale Intuition?

1. Die Rolle rationaler Intuitionin der Geschichte der Philosophie

Philosophen, so schreibt Holm Tetens zu Beginn seines Buches Philosophisches Argumentieren, machen sich nicht die Mühe der Naturwissenschaftler, durch die ganze Welt zu reisen, um ein bestimmtes Phänomen zu beobachten, oder aufwendige Apparaturen zu bauen, um einen bestimmten Effekt nachzuweisen. Philosophen denken einfach nur nach, und das können sie auch im Lehnstuhl tun. Aber was können sie auf diese Weise erkennen? Gibt es wirklich interessante Aussagen, deren Wahrheit man durch bloßes Nachdenken erkennen kann? Diese Frage beschäftigt die Philosophie spätestens, seit Hume behauptet hat, das einzige, war wir durch bloßes Nachdenken erkennen können, seien analytische Wahrheiten.¹⁴ Aber gehen wir zunächst etwas weiter zurück in der Geschichte der Philosophie und der Wissenschaften.¹⁵

Das sowohl für die Wissenschaften als auch für die Philosophie¹⁶ mehr oder weniger allgemein verbindliche Erkenntnismodell war bis weit in die Neuzeit hinein die Geometrie Euklids. Man beginnt mit Definitionen, Postulaten und Axiomen und leitet aus diesen nacheinander alle anderen Lehrsätze der Geometrie ab. Postulate und Axiome gelten dabei als über jeden Zweifel erhaben. Descartes hat diese Grundidee folgendermaßen zum Ausdruck gebracht: Wir beginnen mit intuitiv gewissen, d. h. klaren und deutlichen Prinzipien, die so einleuchtend sind, dass wir an ihrer Wahrheit nicht zweifeln können, um dann aus diesen Prinzipien weitere wahre Aussagen logisch deduktiv abzuleiten. Intuition oder – wie viele heute sagen würden – rationale Intuition ist also eine Methode, auf die wir uns, so Descartes, stützen können und müssen, wenn wir wirkliches Wissen erwerben wollen. Mit Hilfe dieser Methode können wir z. B. die Wahrheit folgender Aussagen erkennen: „Ich existiere“, „Ich denke“, „Ein Dreieck ist von nur drei Linien, die Kugel von einer einzigen Oberfläche begrenzt“ (Regeln III 5), „Gleiches zu Gleichem hinzugetan ergibt Gleiches“ (Prinzipien I 13), „Aus Nichts kann nicht Etwas werden“ (Prinzipien I 18), „Das Vollkommenere kann nicht von etwas Unvollkommenerem hervorgebracht werden“ (Prinzipien I 18), „Es ist unmöglich, dass dasselbe zugleich ist und nicht ist“ (Prinzipien I 49), „Das Geschehene kann nicht ungeschehen werden“ (Prinzipien I 49) und viele andere mehr.

Hume modifiziert dieses Erkenntnismodell auf zweierlei Weise. Erstens unterscheidet er zwei Arten der Erkenntnis – Erkenntnis, die sich auf Beziehungen von Vorstellungen bezieht, und Erkenntnis, bei der es um Tatsachen geht. Hume zufolge kann das Euklidsche Erkenntnismodell nur im ersten Bereich Gültigkeit beanspruchen. Die zweite Modifikation betrifft die Frage, welche Aussagen als intuitiv gewiss gelten können. Hume misstraut der Fähigkeit zur rationalen Intuition, mit deren Hilfe wir vermeintlich auch nicht-analytische Aussagen a priori als wahr erkennen können. Für ihn gilt: Intuitiv gewiss sind nur Aussagen, bei denen die Annahme des Gegenteils einen Widerspruch beinhaltet; heute würden wir sagen: intuitiv gewiss sind nur analytische Wahrheiten. Das hat weitreichende Folgen. Denn mit dieser Festlegung scheiden viele Wahrheiten, die traditionell für absolut unbezweifelbar galten, aus dem Bereich dessen aus, was wir a priori wissen können. Das gilt etwa für das Prinzip „Alles, was zu existieren anfängt, muss einen Grund seiner Existenz haben“. Denn die Annahme des Gegenteils dieses Prinzip beinhaltet, so Hume, keinen Widerspruch, und das Prinzip lässt sich auch nicht aus anderen intuitiv gewissen Aussagen deduktiv ableiten. Die Möglichkeit, das Prinzip durch Bezugnahme auf rationale Intuition zu begründen, kommt bei Hume gar nicht mehr vor.

Humes Skepsis in Bezug auf die Fähigkeit zur rationalen Intuition – die Fähigkeit, nicht-analytische erste Prinzipien intuitiv als wahr zu erkennen – wurde im 19. Jahrhundert durch die Entdeckung der nicht-euklidischen Geometrien auf eindrucksvolle Weise indirekt gestützt. Auch Euklid ging, wie schon gesagt, von einer Reihe von Definitionen, Axiomen und Postulaten aus, um dann aus diesen die Lehrsätze der Geometrie deduktiv abzuleiten. Zu Euklids Axiomen gehören Aussagen wie „Was demselben gleich ist, ist auch einander gleich“ und „Wenn Gleichem Gleiches hinzugefügt wird, sind die Ganzen gleich“ – Aussagen, die man ohne Weiteres für analytisch halten kann. Zu den Axiomen gehört aber auch das berühmte Parallelenaxiom „Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind“ (Euklid 1997, 3). Die äquivalente moderne Formulierung dieses Axioms lautet: „In einer Ebene gibt es zu jeder Geraden g und jedem Punkt S, der nicht auf g liegt, genau eine Gerade, die durch S geht und parallel zu g ist.“

Ist dieses Axiom wirklich intuitiv gewiss? Auf zwei Wegen hat man versucht, eine Antwort auf diese Frage zu finden. Der erste Weg bestand in dem Versuch zu zeigen, dass das Axiom gar nicht benötigt wird, da es sich aus den anderen Axiomen deduktiv ableiten lässt. Beim zweiten Weg dagegen versuchte man nachzuweisen, dass sich – ganz im Sinne Humes – doch ein Widerspruch ergibt, wenn man das Parallelenaxiom durch seine Negation ersetzt. Aber alle diese Versuche scheiterten. Gauß erkannte schließlich die Unlösbarkeit des Problems. Doch erst Lobatschewski veröffentlichte 1826 eine neue – die später so genannte „hyperbolische“ – Geometrie, in der alle Axiome Euklids gelten außer dem Parallelenaxiom. ¹⁷ Auf dieser Grundlage entwickelten sich die nicht-euklidischen Geometrien, bei denen das Parallelenaxiom entweder ganz wegfällt oder durch andere Axiome ersetzt wird, wobei zum Teil auch noch andere Axiome der euklidischen Geometrie in Mitleidenschaft gezogen werden. Die Entdeckung nichteuklidischer Geometrien war nicht nur für die Mathematik, sondern auch für die Grundannahmen des Euklidisch/Cartesischen Erkenntnismodells von entscheidender Bedeutung. Denn sie zeigte, auf welch wackligen Füßen die Annahme steht, es gebe nicht-analytische erste Prinzipien, deren Wahrheit intuitiv eingesehen werden kann.¹⁸

Die frühe Analytische Philosophie stand erkenntnistheoretisch vollständig auf der Seite Humes. Für sie gab es nur zwei Arten von sinnvollen Aussagen –analytische und empirische Aussagen. Die Wahrheit analytischer Aussagen ergibt sich schon aus der Bedeutung der in ihnen vorkommenden sprachlichen Ausdrücke. Empirische Aussagen werden überprüft, indem man z. B. durch Beobachtung untersucht, ob das, was sie behaupten, der Fall ist. In neuerer Zeit mehren sich aber die Stimmen, die bezweifeln, dass das uns zur Verfügung stehende erkenntnistheoretische Instrumentarium wirklich so karg ist. Manche bezweifeln etwa, dass die Sätze der Mathematik tatsächlich analytisch sind, sind aber trotzdem davon überzeugt, dass wir diese Sätze a priori als wahr erkennen können. Da sie auch dem Kantschen Weg misstrauen, stellt sich für sie deshalb die Frage, ob die apriorische Erkenntnis mathematischer Wahrheiten nicht vielleicht doch auf rationaler Intuition beruht. Andere fragen besonders nach den Grundlagen logischer und modaler Erkenntnis. Woher wissen wir eigentlich, dass der Satz vom ausgeschlossenen Widerspruch gilt? Und worauf beruht die Erkenntnis, dass nichts zugleich ein Quadrat und ein Kreis sein kann? Müssen wir nicht auch bei diesen Wahrheiten annehmen, dass ihre Erkenntnis auf rationaler Intuition beruht?

2. BonJour zur Rechtfertigung rationaler Intuition

Ein Autor, der diese Position mit großer Vehemenz vertritt, ist Laurence BonJour. In In Defense of Pure Reason und auch in Epistemology zählt er eine Reihe von Aussagen auf, für die in seinen Augen gilt: a) Wir können die Wahrheit dieser Aussagen a priori erkennen. b) Diese Aussagen sind aber nicht analytisch. Hieraus folgt nach BonJour, dass wir guten Grund haben zu der Annahme: c) Die Wahrheit dieser Aussagen erkennen wir durch rationale Intuition. Das ist in meinen Augen eine absolut vernünftige Argumentationsstrategie, die allerdings auf zwei zentralen Prämissen beruht – den Prämissen a), dass wir die Wahrheit der betreffenden Aussagen tatsächlich a priori erkennen können, und d), dass es zu der Annahme, dass diese Erkenntnis auf rationaler Intuition beruht, keine vernünftige Alternative gibt.

Zur Liste der Aussagen, die BonJour in Blick hat, gehören unter anderem:

1. Logische Aussagen wie „p ∨ ¬p“ und „¬(p ∧ ¬p)“.
2. Mathematische Aussagen wie „2 + 3 = 5“.
3. Nichts kann zugleich eine Kugel und ein Würfel sein.
4. Alle Dreiecke haben drei Seiten.
5. Wenn a länger als b ist und b länger als c, dann ist a länger als c.
6. Nichts kann zugleich ganz rot und ganz grün sein.

Wer wie ich Humes Grundeinstellung nach wie vor genau so überzeugend findet wie die der Vertreter der frühen Analytischen Philosophie, muss sich der Aufgabe stellen zu zeigen, dass zumindest eine der beiden Prämissen a) oder d) nicht zutrifft. Ich werde mich auf die Prämisse d) konzentrieren und damit zugleich die Annahme b) angreifen. Denn ich denke, dass man zeigen kann, dass alle genannten Aussagen tatsächlich doch analytisch sind oder aus analytischen Aussagen durch Deduktion gewonnen werden können.

3. Logische Wahrheiten

Gibt es überhaupt logische Wahrheiten? Sicher werden viele das Gesetz vom ausgeschlossenen Dritten und das Gesetz vom ausgeschlossenen Widerspruch für (notwendig) wahre logische Gesetze halten und den Modus Ponens für eine allgemeingültige Schlussregel; aber inzwischen haben wir gelernt, dass es neben der klassischen Logik viele andere Logiken gibt, in denen zum Teil ganz andere Gesetze und andere Schlussregeln gelten – die intuitionistische Logik, mehrwertige Logiken, die Fuzzy-Logik usw. Fragen wir trotzdem zunächst, wie in der klassischen Logik das Gesetz vom ausgeschlossenen Dritten und das Gesetz vom ausgeschlossenen Widerspruch begründet werden. Die allermeisten werden die Beweise durch Wahrheitstafeln kennen:

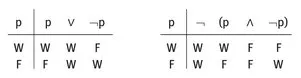
Aber nur wenigen ist klar, dass diese Wahrheitstafeln tatsächlich Beweise für das Gesetz vom ausgeschlossenen Dritten und das Gesetz vom ausgeschlossenen Widerspruch enthalten – Beweise, die sich folgendermaßen explizit machen lassen (ich beschränke mich auf das Gesetz vom ausgeschlossenen Widerspruch).

Ausgangspunkt sind die folgenden klassischen Definitionen der logischen Konstanten „¬“, „∧“ und „∨“:

(¬k)	„¬p“ ist genau dann wahr, wenn p nicht wahr ist.
(∧k)	„p ∧ q“ ist genau dann wahr, wenn p und q beide wahr sind.
(∨k)	„p ∨ q“ ist genau dann wahr, wenn von den Aussagen p und q mindestens eine wahr ist.

Ausgehend von diesen Definitionen lässt sich folgender Beweis führen:

Beweis durch vollständige Fallunterscheidung (es wird vorausgesetzt, dass jede Aussage wahr oder nicht wahr ist)

1. Fall:	Wenn p wahr ist, ist „¬p“ nicht wahr und daher auch „p ∧ ¬p“ nicht wahr; in diesem Fall ist „¬(p ∧ ¬p)“ also wahr.
2. Fall:	Wenn p nicht wahr ist, ist auch „p ∧ ¬p“ nicht wahr; auch in diesem Fall ist „¬(p ∧ ¬p)“ also wahr.

q.e.d.

Auf der Grundlage der angegebenen Definitionen lässt sich das Gesetz vom ausgeschlossenen Widerspruch also problemlos beweisen.¹⁹ Wenn man von anderen Definitionen ausgeht, ergeben sich allerdings andere Resultate. In manchen dreiwertigen Logiken geht man etwa von folgenden Definitionen aus, wobei vorausgesetzt wird, dass jede Aussage einen der drei Wahrheitswerte „wahr“, „falsch“ und „unbestimmt“ hat:

(¬d)	„¬p“ ist wahr, wenn p falsch ist, falsch, wenn p wahr ist und unbestimmt, wenn p unbestimmt ist.
(∧d)	„p ∧ q“ ist wahr, wenn p und q beide wahr sind, falsch, wenn von p und q mindestens eine Aussage falsch ist, und unbestimmt, wenn eine der beiden Aussagen wahr und die andere unbestimmt ist oder wenn beide unbestimmt sind.
(∨d)	„p ∨ q“ ist wahr, wenn von den Aussagen p und q mindestens eine wahr ist, falsch, wenn beide falsch sind, und unbestimmt, wenn eine der beiden Aussagen falsch und die andere unbestimmt ist oder wenn beide unbestimmt sind.

Wenn man von diesen Definitionen ausgeht und davon, dass eine Aussage ein logisches Gesetz ist, wenn sie immer wahr ist – d. h. unabhängig davon, welche Wahrheitswerte ihre Teilaussagen haben –, dann ist leicht zu sehen, dass in der dreiwertigen Logik das Gesetz vom ausgeschlossenen Widerspruch kein logisches Gesetz ist. Denn wenn p den Wahrheitswert unbestimmt hat, dann hat auch nicht „¬p“ und damit auch „p ∧ ¬p“ den Wahrheitswert unbestimmt, und damit hat in diesem Fall auch „¬(p ∧ ¬p)“ den Wahrheitswert unbestimmt.

Zwei Dinge lassen sich also festhalten: 1. Ob eine Aussage ein logisches Gesetz ist, hängt davon ab, wie man die logischen Konstanten definiert.²⁰ 2. Auf der Grundlage dieser Definitionen lässt sich dann aber in der Regel leicht beweisen, dass eine Aussage – gegeben diese Definitionen – ein logisches Gesetz ist oder eben nicht. Es gibt also keinen Grund für die Annahme, dass man zur „Erkenntnis“ logischer Gesetze auf rationale Intuition angewiesen ist.

4. Mathematische Aussagen

Für mathematische Wahrheiten gilt zunächst dasselbe wie für logische Gesetze. Denn, wie das Beispiel der Geometrie schon gezeigt hat, kommt es auch hier darauf an, von welchen Voraussetzungen – z. B. von welchen Axiomen – man ausgeht. Dabei denkt heute meines Wissens kein Mathematiker mehr, dass eines dieser Axiomensysteme selbst als wah...

Table of contents

• Titel
• Impressum
• Inhaltsverzeichnis
• Vorwort
• Kurzzusammenfassungen der Beiträge
• Warum Philosophie?
• Philosophisches Argumentieren
• Wissen, Verstehen und Sprache
• Letzte Fragen
• Index