Finanzmathematik

Lehrbuch mit Übungen

Jutta Arrenberg

• Publisher: De Gruyter Oldenbourg
• Year: 2015
• eBook ISBN: 9783110423785
• Edition: 3
• Topic: Commerce
• Subtopic: Mathématiques d'entreprise

Klar strukturiert vermittelt dieses Lehr- und Übungsbuch die Grundlagen der Finanzmathematik. Behandelt werden verschiedene übliche Verzinsungsarten, Rentenrechnung, Tilgungsrechnung, Investitionsrechnung, Abschreibungsverfahren sowie die effektive Verzinsung.
Die dritte Auflage wurde erweitert durch Formeln der Finanzmathematik im Tabellenkalkulator Excel, und am Ende eines jeden Kapitels wurde eine Formelsammlung erstellt.

1 Einführung

Aufgabe der Finanzmathematik ist es, für langwierige Zahlungsvorgänge kurze, prägnante Berechnungsformeln zu entwickeln, mit deren Hilfe gewünschte Ergebnisse undVergleiche schnell und bequem berechnet werden können. Wir beschäftigen uns in diesem Buch mit der Herleitung solcher Berechnungsformeln.

Bevor wir mit dem f i nanzmathematischen Rechnen beginnen, legen wir die zukünftige Notation fest. Gemessen an den vielen Formeln, die wir später erarbeiten werden,umfasst die Notation nur einige wenige Bezeichnungen.

Definition 1.1

K0	Anfangskapital
Kn	Endkapital nach n Jahren
n	Laufzeit in Jahren
p	Zinsfuß pro anno (bei 4% Jahreszinsen beträgt p = 4)
i	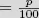Zinssatz pro anno (bei 4% Jahreszinsen beträgt i = 0,04)
q	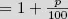Zinsfaktor pro anno (bei 4% Jahreszinsen beträgt q = 1,04)

Neben diesen sechs Bezeichnungen spielen die folgenden beiden Rechenoperationen inder Finanzmathematik eine zentrale Rolle: Mit dem Begriff Aufzinsen wird die Rechenoperation bezeichnet, die von K₀ zu K_n führt. Mit dem Begriff Abzinsen wirdhingegen die Rechenoperation bezeichnet, die von K_n zu K₀ führt.

Zum Lösen einer Aufgabe hat es sich als sehr hilfreich herausgestellt, wenn die Zahlungsströme auf einer Zeitachse dargestellt werden. Dazu werden die Jahreszahlen mittigzwischen zwei senkrechte Begrenzungsstriche auf der Zeitachse eingetragen. Die Geld-beträge werden zum Fälligkeitszeitpunkt mit senkrechten Pfeilen – bei Einzahlungennach unten gerichtet und bei Auszahlungen nach oben gerichtet – markiert:

Beispiel 1.2

Ein Konto hat die folgenden Zahlungsbewegungen:

• sofortige Einzahlung von 5000 GE

• Auszahlung von 1000 GE nach drei Jahren

• Einzahlung von 2000 GE nach fünf Jahren

Um den Kontostand nach sechs Jahren erfassen zu können, wird erst einmal dieZeitachse mit den Zahlungsströmen angelegt:

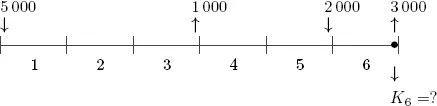
Um jetzt den Kontostand am Ende des sechsten Jahres berechnen zu können, wirdneben dem Jahreszins die Verzinsungsart benötigt.

In der Finanzmathematik werden im Wesentlichen zwei Zinsarten unterschieden: Imersten Fall gibt es keine Zinsen auf Zinsen, d.h. Bemessungsgrundlage für die jährlicheZinshöhe ist immer das Startkapital, diese Zinsen werden in der Finanzmathematik als einfache Zinsen bezeichnet. Im zweiten Fall werden die Vorjahreszinsen im nächstenJahr mit verzinst, diese Zinsen werden in der Finanzmathematik als Zinseszinsen bezeichnet.

2 Einfache Zinsen

Bei der Verzinsung mit einfachen Zinsen ist der Endwert Kn eine lineare Funktion der Laufzeit n. Deshalb wird die Verzinsung mit einfachen Zinsen auch als lineare Verzinsung bezeichnet.

Mit der linearen Verzinsung werden z.B. Kapitalschulden für Zwecke der Erbschaft- und Schenkungsteuer bewertet.

Wie wir später in Kapitel 3.3 noch sehen werden, wird die lineare Verzinsung herangezogen, um Jahresbruchteile bei der gemischten Verzinsung zu verzinsen.

2.1 Lineare Verzinsung

Hauptaufgabe der linearen Verzinsung ist es, den Betrag auszurechnen, auf den ein Kapital von K0 Geldeinheiten (GE) in n Jahren angewachsen sein wird, wenn für die Verzinsung zu p % pro anno jeweils das Anfangskapital K0 zur Bemessung zu Grunde gelegt wird.

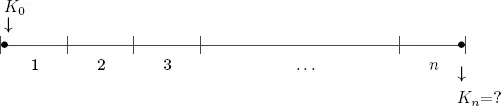
Die Zinsen sind jedes Jahr gleich groß, da sie immer bezogen auf das Anfangskapital berechnet werden. Nach einem Jahr ergeben sich folgende Beträge:

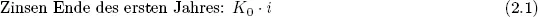
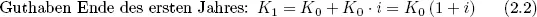
Nach einem weiteren Jahr ergeben sich folgende Beträge:

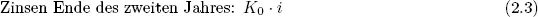
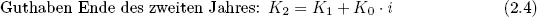
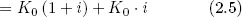
Bei einer Laufzeit von n Jahren ergibt sich folgender Verzinsungsplan:

Definition 2.1

Jahr	Zinsen am Ende des Jahres	Guthaben am Ende des Jahres
1	K0· i	K1 = K0 (1 + i)
2	K0· i	K2 = K0 (1 + 2 · i)
3	K0· i	K3 = K0 (1 + 3 · i)
. . .
n	K0· i	Kn = K0 (1 + n · i)

In der Definition 2.1 lässt sich insb. erkennen, dass bei der linearen Verzinsung das Endkapital Kn linear abhängt von der Laufzeit n.

Beispiel 2.2

Eine Stude...

Table of contents

• Cover
• Title
• Copyright
• Table of Contents
• Preface
• 1 Einführung
• 2 Einfache Zinsen
• 3 Zinseszinsen
• 4 Rentenrechnung
• 5 Tilgungsrechnung
• 6 Effektivzins
• 7 Investitionsrechnung
• 8 Abschreibungsverfahren
• 9 übungen
• A Anhang
• Index