Strukturgleichungsmodelle in den Sozialwissenschaften

Jost Reinecke

• Publisher: De Gruyter Oldenbourg
• Year: 2014
• eBook ISBN: 9783110396980
• Edition: 2
• Topic: Social Sciences
• Subtopic: Sociology
• Index: Social Sciences

Das Buch gibt eine Einführung in die methodologischen und statistischen Grundlagen von Strukturgleichungsmodellen und in deren Handhabung für sozialwissenschaftliche Forschungsfragestellungen. Neben historischen Betrachtungen wird auf Basis verschiedener Erhebungsdesigns eine Einführung in die Pfadanalyse, in Messmodelle, in die konformatorische Faktorenanalyse bis zum allgemeinen Strukturgleichungsmodell vorgenommen. Neben der formalen Darstellung der einzelnen Modellvarianten steht die Erörterung anhand empirischer Beispiele im Vordergrund. Damit kann auch der statistisch weniger versierte Leser die Modellierungen nachvollziehen und auf seine eigenen Fragestellungen übertragen. In den letzten Jahren hat sich in sozialwissenschaftlichen Anwendungsbereichen eine Reihe spezieller Modellierungen mit Strukturgleichungen etabliert. Hierzu gehören Wachstums- und Mischverteilungsmodelle, die in Form eines eigenen Kapitels in die zweite Auflage aufgenommen wurden. Um eine zur EDV-Umgebung des jeweiligen Nutzers passende Auswahl treffen zu können, werden zur Verfügung stehende Programme zur Berechnung von Strukturgleichungsmodellen mit ihren jeweiligen Aktualisierungen erörtert. Weiterführende Hinweise aus dem Internet werden an den jeweiligen Stellen angegeben. Die Literaturliste wurde für die zweite Auflage umfassend ergänzt und aktualisiert.

1 Einleitung

Mit dem Begriff Strukturgleichungsmodelle wird nicht nur eine einzelne Technik, sondern eine ganze Gruppe von Modellen multivariater, statistischer Datenanalysen bezeichnet. Kovarianzstrukturanalyse oder Kovarianzstrukturmodelle sind alternative Begrifflichkeiten, die in der Literatur verwendet werden. Verschiedene charakteristische Eigenschaften können in der folgenden Systematisierung genannt werden:

1. Strukturgleichungsmodelle werden nach Formulierung bestimmter inhaltlicher Hypothesen aufgestellt und überprüft. Hiermit wird der konfirmatorische Charakter dieser statistischen Modellbildung hervorgehoben: Das Modell stellt eine Verknüpfung inhaltlicher Zusammenhangshypothesen dar, die anhand empirisch gewonnener Daten getestet werden. Demgegenüber würde ein aus den Daten generiertes Modell eine explorative Modellstrategie unterstützen. Jöreskog und Sörbom (1993a) unterscheiden drei typische Situationen der Modellprüfung:
   • Eine strikt konfirmatorische Prüfung, wobei der Forscher einen einzelnen Modelltest vornimmt und die zugrunde liegenden Hypothesen entweder bestätigt oder verwirft.
   • Eine konfirmatorische Prüfung von Modellen, bei der der Forscher mehrere alternative Hypothesen überprüft und sich für ein zu akzeptierendes Modell entscheidet.
   • Eine modellgenerierte Anwendung, bei der der Forscher ein Anfangsmodell (sogenanntes initial model) spezifiziert und durch schrittweise Modellmodifikation eine Annäherung an die Datenstruktur erreicht.
   Die zuletzt genannte Strategie wird in der Praxis am häufigsten durchgeführt und verfolgt zwei Ziele: Zum einen soll das Modell entwickelt werden, das am ehesten den theoretischen Überlegungen entspricht, zum anderen soll auch eine hohe statistische Korrespondenz zwischen dem Modell und den Daten gewährleistet sein.
2. Strukturgleichungsmodelle können explizit nach gemessenen (sogenannten manifesten) und nicht gemessenen (sogenannten latenten) Variablen unterscheiden und erlauben eine Differenzierung in ein Meß- und ein Strukturmodell. Die explizite Formulierung eines Meßmodells ermöglicht die Berücksichtigung unterschiedlicher Meßqualitäten der manifesten Variablen, vorausgesetzt die latenten Variablen werden über mehr als eine gemessene Variable definiert. Das Meßmodell führt zu einer sogenannten minderungskorrigierten Schätzung der Zusammenhänge zwischen den latenten Variablen. Dies bedeutet, daß sich die Konstruktvalidität der einzelnen Messungen explizit auf die Koeffizienten des Strukturmodells auswirkt. Für das klassische Pfadmodell wird kein Meßmodell formuliert. Die postulierten Beziehungen der manifesten Variablen werden geschätzt, ohne daß die Konstruktvalidität der Messungen geprüft wird. In der Regel werden dadurch die geschätzten Koeffizienten des klassischen Pfadmodells unterschätzt.
3. Die meisten Strukturgleichungsmodelle basieren auf Befragungsdaten, die nicht experimentell erhoben werden. Werden experimentelle oder quasi-experimentelle Anordnungen vorgenommen, dann lassen sich über Gruppenbildungen Differenzen der Modellparameter ermitteln. Dabei können Strukturgleichungsmodelle über die Leistungsfähigkeit der klassischen Varianzanalyse hinausgehen, weil eine Differenzierung in manifeste und latente Variablen dort nicht möglich ist.
4. Mit Strukturgleichungsmodellen werden große Datensätze analysiert. Es ist relativ schwierig, eine einfache Antwort auf die Frage zu geben, wie hoch die Mindestgröße der Stichprobe sein muß, um stabile Parameterschätzungen in Strukturgleichungsmodellen zu erhalten. Ein deutlicher Zusammenhang besteht zwischen der Stichprobengröße und der Modellkomplexität: Je mehr Parameter im Modell zu schätzen sind, desto größer muß die Datenbasis sein. Des weiteren werden bei Schätzverfahren, die höhere Momente berücksichtigen, größere Stichproben benötigt.
5. Varianzen und Kovarianzen bilden in der Regel die Datengrundlage für Strukturgleichungsmodelle. Damit werden zwei Ziele verbunden. Zum einen die Uberprüfung der Zusammenhänge zwischen den Variablen auf Grund der postulierten Hypothesen und zum anderen die Erklärung der Variationen in den abhängigen Variablen. Werden über Kovariaten (z. B. Geschlecht) Gruppen gebildet, dann können Unterschiede der Modellparameter zwischen den Gruppen ermittelt und getestet werden. Mittelwertdifferenzen können zwischen den latenten Variablen geschätzt werden, wenn neben den Varianzen und Kovarianzen auch der Mittelwertvektor der manifesten Variablen zur Verfügung steht.
6. Viele statistische Techniken wie die Varianzanalyse, die multiple Regression oder die Faktorenanalyse sind spezielle Anwendungen von Strukturgleichungsmodellen. Schon vor längerer Zeit konnte festgestellt werden, daß die Varianzanalyse (ANO-VA) ein Spezialfall der multiplen Regression ist und beide Verfahren wiederum unter das allgemeine lineare Modell eingeordnet werden können. Zum allgemeinen linearen Modell gehören auch die multivariate Varianzanalyse (MANOVA) und die exploratorische Faktorenanalyse. Alle Varianten des allgemeinen linearen Modells sind in Strukturgleichungsmodelle überführbar. Durch nicht-lineare Parameterrestriktionen können Produktterme in den linearen Gleichungen berücksichtigt werden. Dies führt beispielsweise zu sogenannten Interaktionsmodellen.
7. Strukturgleichungsmodelle beschränken sich nicht nur auf kontinuierliche Variablen. Kategoriale Variablen können in den Modellen gleichermaßen berücksichtigt werden. Multinomiale Regressionsmodelle können Teil eines komplexeren Strukturgleichungsmodells sein. Wenn latenten kategoriale Variablen berücksichtigt werden, so haben diese die Funktion, Subgruppen als latente Klassen zu identifizieren und damit Hinweise auf unbeobachtete Heterogenität im Datenmaterial zu geben.

Mit dem Begriff Strukturgleichungsmodelle wird ein sehr breites Feld multivariater statistischer Datenanalysen angesprochen, dessen einzelne Facetten in einem Lehrbuch nicht alle abgedeckt werden können. Das vorliegende Lehrbuch konzentriert sich deswegen einerseits auf die Vermittlung fundamentaler Konzepte und andererseits auf die Erarbeitung von Techniken, die Hypothesentests mit unterschiedlichen Datendesigns erlauben.

 

Dieses Lehrbuch gliedert sich in acht Kapitel. In Kapitel 2 wird zunächst ein Überblick über die Entwicklung der statistischen Modellbildung mit Strukturgleichungen gegeben. Hierzu gehört die generelle Vorgehensweise bei der Anwendung dieser Modelle, ihre methodischen Eigenschaften als auch die Frage, unter welchen Bedingungen den ermittelten Parametern eine kausale Bedeutung zukommt. Abschließend wird ein Überblick über die methodischen Entwicklungen der letzten Jahre gegeben, die auch zu einer Differenzierung der einzelnen Modellarten geführt haben. Kapitel 3 differenziert die in der empirischen Sozialforschung bekannten Erhebungsdesigns (Querschnitt und Längsschnitt) und erläutert, welche Arten von Strukturgleichungsmodellen mit welchen Daten in den nachfolgenden Kapiteln behandelt werden. Kapitel 4 geht auf grundlegende statistische Konzepte für Strukturgleichungsmodelle ein. Hier werden zunächst das Meßniveau der Variablen behandelt und die gängigen statistischen Zusammenhangsmaße. Die lineare Regressionsanalyse gilt gemeinhin als grundlegend für die Modellbildung mit Strukturgleichungen, während die klassische Testtheorie das mathematische Modell zur Berücksichtigung von Meßfehlern liefert. Beide Ansätze werden hier in ihren Grundzügen erörtert.

 

Die Kapitel 5, 6, 7, 8 und 9 behandeln die einzelnen Modellarten. Beispiele aus Querschnitt- und Längsschnittuntersuchungen werden jeweils diskutiert, ebenso die gleichzeitige Analyse über mehrere Untersuchungsgruppen (multiple Gruppenvergleiche). In Kapitel 5 geht es ausschließlich um Modelle mit gemessenen Variablen, die auch als Pfadmodelle bezeichnet werden. Die Differenzierung in gemessene (manifeste) und nicht gemessene (latente) Variablen erfolgt in Kapitel 6 über die Erörterung der Meßmodelle, wobei an dieser Stelle auch eine ausführliche Diskussion der einzelnen Schätzverfahren sowie die damit verbundenen Statistiken der Modellprüfung vorgenommen wird. Beide sind von grundsätzlicher Bedeutung für alle in diesem Buch behandelten Modelle. In Kapitel 7 wird das Meßmodell zum konfirmatorischen Faktorenmodell erweitert, während Kapitel 8 in den allgemeinen Strukturgleichungsansatz einführt. Hier wird das zuvor diskutierte konfirmatorische Faktorenmodell um ein Strukturmodell, das die Beziehung zwischen den latenten Variablen formalisiert, erweitert. Spezifische Aspekte der Modellbildung beim multiplen Gruppenvergleich, bei kategorialen Variablen und bei Längsschnittdaten werden hier behandelt. Techniken zur Berücksichtigung von fehlenden Werten bei der Berechnung von Strukturgleichungsmodellen stehen hier ebenfalls im Vordergrund. In Kapitel 9 werden Wachstums- und Mischverteilungsmodelle erörtert, die mittlerweile durch die zunehmende Verbreitung von Paneldaten nicht nur in der methodischen und statistischen Grundlagenforschung, sondern auch in vielen inhaltlichen Anwendungen einen breiten Raum eingenommen haben.

 

In Kapitel 10 werden EDV-Programme zur Berechnung von Strukturgleichungsmodellen vorgestellt. Hierzu gehören auch Übersichten über die Notation der Variablen, Parameter und Matrizen. Die zur Ersetzung fehlender Werte verwendeten Programme werden an dieser Stelle zusätzlich erläutert. Das Literatur- und Stichwortverzeichnis sollen die Handhabung dieses Lehrbuchs vereinfachen.

2 Die Entwicklung der statistischen Modellbildung mit Strukturgleichungen

2.1 Einführung

Die Verfahren, die eine statistische Modellbildung voraussetzen und unter dem Begriff Strukturgleichungsmodelle gefaßt werden, ermöglichen strengere Tests formalisierter Hypothesen als die üblichen Verfahren der bivariaten und multivariaten Statistik.² Anwendungen sind besonders in den Wissenschaftsbereichen zu verzeichnen, die größere Datenmengen auf der Basis eines quasi-experimentellen oder nicht-experimentellen Designs produzieren. Stabile Ergebnisse aus statistischen Modellbildungen mit Strukturgleichungen sind dann gewährleistet, wenn bestimmte Meß- und Verteilungsvoraussetzungen gemacht werden können und wenn, in Abhängigkeit von der Modellgröße, die empirischen Informationen auf einer ausreichenden Anzahl von Untersuchungseinheiten basieren.

Die Verbreitung von Strukturgleichungsmodellen in den angewandten Sozialwissenschaften ist ohne ökonometrische und psychometrische Grundlagen kaum vorstellbar. Inhaltliche Spezifikationen von Beziehungen zwischen unabhängigen und abhängigen Variablen, wie sie aus der multiplen Regressionsanalyse bekannt sind, bilden den Ausgangspunkt (vgl. Kapitel 4). Jedes Regressionsmodell beinhaltet bekanntermaßen eine abhängige Variable und mindestens eine unabhängige Variable, deren Verhältnis über eine Regressionsgleichung formalisiert wird. Werden mehrere Regressionsmodelle miteinander verbunden, dann wird diese Art der Modellierung als Pfadanalyse bezeichnet (vgl. Kapitel 5). Diese weitergehende Modellierung ist erstmals von dem Genetiker Wright (1921, 1934) vorgenommen worden, der auch die Allgemeingültigkeit der Zerlegung von Produkt-Moment-Korrelationen in sogenannte Pfadkoeffizienten über das Basistheorem der Pfadanalyse nachweisen konnte (vgl. O. D. Duncan, 1966, S. 5; Kenny, 1979, S. 28).³

Abb. 2.1: Pfadmodell mit drei Variablen

Für ein Pfadmodell mit drei Variablen x₁, x₂ und x₃ kann dieses Basistheorem leicht erläutert werden (vgl. Abbildung 2.1). Hierzu werden für jede abhängige Variable eine lineare Gleichung formuliert:

(2.1)

(2.2)

Sind ausreichende empirische Informationen (Korrelationskoeffizienten) vorhanden, dann lassen sich sich beispielsweise die Korrelationen zwischen x₁ und x₃ (r₃₁), x₂ und x (r) sowie in die entsprechenden Pfadkoeffizienten p₂₁, p₃₁ und p₃₂ zerlegen:⁴

(2.3)

(2.4)

Beispielsweise wird aus Gleichung 2.3 ersichtlich, daß die Korrelation r nicht nur durch den direkten Effekt der Variablen x₁ auf die Variable x₃ (p₃₁) bestimmt wird, sondern auch durch den indirekten Effekt über die vermittelnde Variable x₂. Dieser indirekte Effekt wird aus dem Produkt der Pfadkoeffizienten p₂₁ und p₃₂ gebildet. Diese Zerlegung ist allgemeingültig und unabhängig von der Modellgröße.

Blalock (1961) gehört zu den ersten, der die Pfadanalyse in den Sozialwissenschaften thematisiert. Anwendungen insbesondere mit Variablen aus der Sozialstrukturanalyse finden sich bei O. D. Duncan und Hodge (1963), O. D. Duncan (1966) sowie ausführlich in dem Buch von Blau und Du...

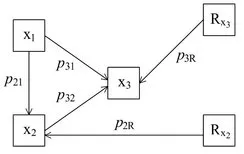
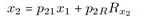
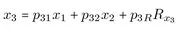
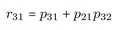
Table of contents

• Titel
• Impressum
• Vorwort
• Inhaltsverzeichnis
• 1 Einleitung
• 2 Die Entwicklung der statistischen Modellbildung mit Strukturgleichungen
• 3 Erhebungsdesigns, Daten und Modelle
• 4 Statistische Grundlagen für Strukturgleichungsmodelle
• 5 Strukturgleichungsmodelle mitgemessenen Variablen
• 6 Meßmodelle
• 7 Die konfirmatorische Faktorenanalyse
• 8 Das allgemeine Strukturgleichungsmodell
• 9 Wachstums- und Mischverteilungsmodelle
• 10 EDV-Programme
• Literaturverzeichnis
• Index