Algorithmische Graphentheorie

Volker Turau, Christoph Weyer

• Publisher: De Gruyter
• Year: 2015
• Print ISBN: 9783110417272
• eBook ISBN: 9783110420005
• Edition: 4
• Topic: Mathematics
• Subtopic: Computer Science General
• Index: Mathematics

Jedes System, das aus diskreten Zuständen oder Objekten und Beziehungen zwischen diesen besteht, kann als Graph modelliert werden.

Diese Darstellung ermöglicht den Einsatz graphentheoretischer Algorithmen. Das vorliegende Buch stellt die grundlegenden Algorithmen zur Lösung graphentheoretischer Problemstellungen anhand praktischer Beispiele aus der Informatik vor. Die Algorithmen sind in kompakter Form in einer programmiersprachennahen Notation dargestellt, die eine Übertragung in eine konkrete Implementierung leicht macht. Die praktische Relevanz der behandelten Algorithmen wird in vielen Anwendungen aus Gebieten wie Compilerbau, Künstlicher Intelligenz, Betriebssystemen, Computernetzwerken, Suchmaschinen, Analyse sozialer Netzwerke und Operations Research demonstriert. Elf Kapitel decken die wichtigsten Teilgebiete der Algorithmischen Graphentheorie ab. Die vorliegende vierte, erweiterte und überarbeitete Auflage des Buches zeichnet sich unter anderem durch ein neues umfangreiches Kapitel über Entwurfsmethoden der Algorithmischen Graphentheorie aus.

Das Buch enthält 280 Übungsaufgaben in verschiedenen Schwierigkeitsgraden, für das Bachelor- und das Masterstudium. Die ausführlichen Lösungen können kostenlos bezogen werden.

KAPITEL 1

Einleitung

In vielen praktischen und theoretischen Anwendungen treten Situationen auf, die durch ein System von Objekten und Beziehungen zwischen diesen Objekten charakterisiert werden können. Die Graphentheorie stellt zur Beschreibung von solchen Systemen einModell zur Verfügung: den Graphen. Die problemunabhängige Beschreibung mittels eines Graphen lässt die Gemeinsamkeit von Problemen aus den verschiedensten Anwendungsgebieten erkennen. Die Graphentheorie ermöglicht somit die Lösung vieler Aufgaben, welche aus dem Blickwinkel der Anwendung keine Gemeinsamkeiten haben. Die algorithmische Graphentheorie stellt zu diesem Zweck Verfahren zur Verfügung, die problemunabhängig formuliert werden können. Ferner erlauben Graphen eine anschauliche Darstellung, welche die Lösung von Problemen häufig erleichtert.

Im Folgenden werden sechs verschiedene Anwendungen diskutiert. Eine genaue Betrachtung der Aufgabenstellungen führt ganz natürlich auf eine graphische Beschreibung und damit auch auf den Begriff des Graphen; eine Definition wird bewusst erst im nächsten Kapitel vorgenommen. Die Beispiele dienen als Motivation für die Definition eines Graphen; sie sollen ferner einen Eindruck von der Vielfalt der zu lösenden Aufgaben geben und die Notwendigkeit von effzienten Algorithmen vor Augen führen.

1.1 Verletzlichkeit von Kommunikationsnetzen

Ein Kommunikationsnetz ist ein durch Datenübertragungswege realisierter Verband mehrerer Rechner. Es unterstützt den Informationsaustausch zwischen Benutzern an verschiedenen Orten. Die Verletzlichkeit eines Kommunikationsnetzes ist durch die Anzahl von Leitungen oder Rechnern gekennzeichnet, die ausfallen müssen, damit die Verbindung zwischen zwei beliebigen Benutzern nicht mehr möglich ist. Häfig ist eine Verbindung zwischen zwei Benutzern über mehrere Wege möglich. Somit ist beim Ausfall einer Leitung oder einer Station die Verbindung nicht notwendigerweise unterbrochen. Ein Netzwerk, bei dem schon der Ausfall einer einzigen Leitung oder Station gewisse Verbindungen unmöglich macht ist verletzlicher, als ein solches, wo dies nur beim Ausfall von mehreren Leitungen oder Stationen möglich ist.

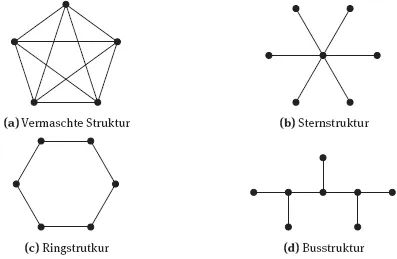
Die minimale Anzahl von Leitungen und Stationen, deren Ausfall die Funktion des Netzwerkes beeinträchtigt, hängt sehr stark von der Beschaffenheit des Netzwerkes ab. Netzwerke lassen sich graphisch durch Knoten und Verbindungslinien zwischen den Knoten darstellen: Die Knoten entsprechen den Stationen, die Verbindungslinien den Datenübertragungswegen. In Abbildung 1.1 sind vier Grundformen gebräuchlicher Netzwerke dargestellt.

Abb. 1.1: Netzwerktopologien

Bei der vermaschten Struktur ist beim Ausfall einer Station die Kommunikation zwischen den restlichen Stationen weiter möglich. Sogar der Ausfall von bis zu sechs Datenübertragungswegen muss noch nicht zur Unterbrechung führen. Um die Kommunikation mit einem Benutzer zu unterbrechen, müssen mindestens vier Datenübertragungswege ausfallen. Bei der Sternstruktur ist nach dem Ausfall der zentralen Station keine Kommunikation mehr möglich. Hingegen führt in diesem Fall der Ausfall einer Leitung nur zur Abkopplung eines Benutzers.

Eine Menge von Datenübertragungswegen in einem Kommunikationsnetzwerk heißt Schnitt, falls ihr Ausfall die Kommunikation zwischen irgendwelchen Stationen unterbricht. Ein Schnitt mit der Eigenschaft, dass keine echte Teilmenge ebenfalls ein Schnitt ist, nennt man minimaler Schnitt. Die Anzahl der Verbindungslinien in dem minimalen Schnitt mit den wenigsten Verbindungslinien nennt man Verbindungszusammenhang oder auch die Kohäsion des Netzwerkes. Sie charakterisiert die Verletzlichkeit eines Netzwerkes. Die Kohäsion der Bus- und Sternstruktur ist gleich 1, die der Ringstruktur gleich 2, und die vermaschte Struktur hat die Kohäsion 4.

Analog kann man auch den Begriff Knotenzusammenhang eines Netzwerkes denieren. Er gibt die minimale Anzahl von Stationen an, deren Ausfall die Kommunikation der restlichen Stationen untereinander unterbrechen würde. Bei der Bus- und Sternstruktur ist diese Zahl gleich 1 und bei der Ringstruktur gleich 2. Fällt bei der vermaschten Struktur eine Station aus, so bilden die verbleibenden Stationen immer noch eine vermaschte Struktur. Somit ist bei dieser Struktur beim Ausfall von beliebig vielen Stationen die Kommunikation der restlichen Stationen gesichert.

Verfahren zur Bestimmung von Verbindungszusammenhang und Knotenzusammenhang eines Netzwerkes werden in Kapitel 9 behandelt.

1.2 Wegplanung Für Roboter

Ein grundlegendes Problem auf dem Gebiet der Robotik ist die Planung von kollisionsfreien Wegen für Roboter in ihrem Einsatzgebiet. Von besonderem Interesse sind dabei die kürzesten Wege, auf denen der Roboter mit keinem Hindernis in Kontakt kommt. Zum Auffnden dieserWege muss eine Beschreibung der Geometrie des Roboters und des Einsatzgebietes vorliegen. Ohne Einschränkungen der Freiheitsgrade des Roboters und der Komplexität des Einsatzgebietes ist dieses Problem praktisch nicht lösbar.

Abb. 1.2: Hindernisse Für einen Roboter

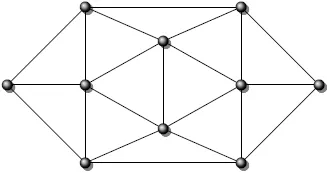
Eine stark idealisierte Version dieses komplizierten Problems erhält man, indem man die Bewegung auf eine Ebene beschränkt und den Roboter auf einen Punkt reduziert. Diese Ausgangslage kann auch in vielen Anwendungen durch eine geeignete Transformation geschaffen werden. Das Problem stellt sich nun folgendermaßen dar: Für eine Menge von Polygonen in der Ebene, einen Startpunkt s und einen Zielpunkt z ist der kürzeste Weg von s nach z gesucht, welcher die Polygone nicht schneidet; Abbildung 1.2 zeigt eine solche Situation.

Zunächst wird der kürzeste Weg analysiert, um dann später ein Verfahren zu seiner Bestimmung zu entwickeln. Dazu stellt man sich den kürzesten Weg durch ein straff gespanntes Seil vor. Es ergibt sich sofort, dass derWeg eine Folge von Geradensegmenten der folgenden Art ist:

(1) Geradensegmente von s oder z zu einer konvexen Ecke eines Hindernisses, welche keine anderen Hindernisse schneiden

(2) Kanten von Hindernissen zwischen konvexen Ecken

(3) Geradensegmente zwischen konvexen Ecken von Hindernissen, welche keine anderen Hindernisse schneiden

(4) das Geradensegment von s nach z, sofern kein Hindernis davon geschnitten wird

Für jede Wahl von s und z ist der kürzeste Weg eine Kombination von Geradensegmenten der oben beschriebenen vier Typen. Der letzte Typ kommt nur dann vor, wenn die direkte Verbindung von s und z kein Hindernis schneidet; in diesem Fall ist dies auch der kürzeste Weg. Abbildung 1.3 zeigt alle moglichen Geradensegmente Für die Situation aus Abbildung 1.2.

Abb. 1.3: Geradensegmente Für den kürzesten Weg

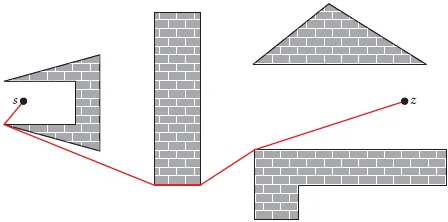
Um einen kürzesten Weg von s nach z zu finden, mussen im Prinzip alle Wege von s nach z, welche nur die angegebenen Segmente verwenden, betrachtet werden. Für jeden Weg ist dann die Länge zu bestimmen, und unter allenWegen wird der kürzeste ausgewählt. Das Problem lässt sich also auf ein System von Geradensegmenten mit entsprechenden Längen reduzieren. In diesem ist dann ein kürzesterWeg von s nach z zu finden. Die Geradensegmente, die zu diesem System gehören, sind in Abbildung 1.3 blau eingezeichnet. Abbildung 1.4 zeigt den kürzesten Weg von s nach z. Verfahren zur Bestimmung von kürzesten Wegen in Graphen werden in Kapitel 10 behandelt.

Abb. 1.4: Der kürzeste Weg von s nach z

1.3 Optimale Umrustzeiten Für Fertigungszellen

Die Maschinen einer Fertigungszelle in einer Produktionsanlage müssen für verschiedene Produktionsaufträge unterschiedlich ausgerüstet und eingestellt werden. Während dieser Umrüstzeit kann die Fertigungszelle nicht produktiv genutzt werden. Aus diesem Grund wird e...

Table of contents

• Cover
• Titel
• Impressum
• Inhalt
• 1 Einleitung
• 2 Einführung
• 3 Bäume
• 4 Suchverfahren in Graphen
• 5 Entwurfsmethoden für die algorithmische Graphentheorie
• 6 Färbung von Graphen
• 7 Perfekte Graphen
• 8 Flüsse in Netzwerken
• 9 Anwendungen von Netzwerkalgorithmen
• 10 Kürzeste Wege
• 11 Approximative Algorithmen
• Die Graphen an den Kapitelanfängen
• Literatur
• Index