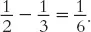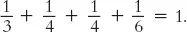Measurement

Paul Lockhart

• Publisher: Belknap Press
• Year: 2012
• ISBN:
  9780674071179
• Topic: Mathematics
• Subtopic: Mathematics General
• Index: Mathematics

For seven years, Paul Lockhart's A Mathematician's Lament enjoyed a samizdat-style popularity in the mathematics underground, before demand prompted its 2009 publication to even wider applause and debate. An impassioned critique of K–12 mathematics education, it outlined how we shortchange students by introducing them to math the wrong way. Here Lockhart offers the positive side of the math education story by showing us how math should be done. Measurement offers a permanent solution to math phobia by introducing us to mathematics as an artful way of thinking and living.In conversational prose that conveys his passion for the subject, Lockhart makes mathematics accessible without oversimplifying. He makes no more attempt to hide the challenge of mathematics than he does to shield us from its beautiful intensity. Favoring plain English and pictures over jargon and formulas, he succeeds in making complex ideas about the mathematics of shape and motion intuitive and graspable. His elegant discussion of mathematical reasoning and themes in classical geometry offers proof of his conviction that mathematics illuminates art as much as science.Lockhart leads us into a universe where beautiful designs and patterns float through our minds and do surprising, miraculous things. As we turn our thoughts to symmetry, circles, cylinders, and cones, we begin to see that almost anyone can "do the math" in a way that brings emotional and aesthetic rewards. Measurement is an invitation to summon curiosity, courage, and creativity in order to experience firsthand the playful excitement of mathematical work.

PART ONE

SIZE AND SHAPE

1

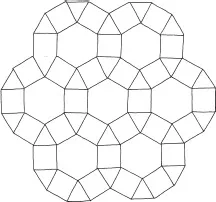
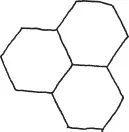
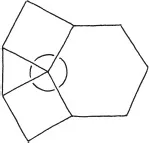
Here is a nice pattern.

Let me tell you why I find this kind of thing so attractive. First of all, it involves some of my favorite shapes.

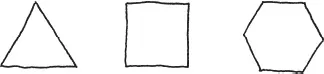
I like these shapes because they are simple and symmetrical. Shapes like these that are made of straight lines are called polygons (Greek for “many corners”). A polygon with all its sides the same length and all its angles equal is called regular. So I guess what I’m saying is, I like regular polygons.

Another reason why the design is appealing is that the pieces fit together so nicely. There are no gaps between the tiles (I like to think of them as ceramic tiles, like in a mosaic), and the tiles don’t overlap. At least, that’s how it appears. Remember, the objects that we’re really talking about are perfect, imaginary shapes. Just because the picture looks good doesn’t mean that’s what is really going on. Pictures, no matter how carefully made, are part of physical reality; they can’t possibly tell us the truth about imaginary, mathematical objects. Shapes do what they do, not what we want them to do.

So how can we be sure that the polygons really do fit perfectly? For that matter, how can we know anything about these objects? The point is, we need to measure them—and not with any clumsy real-world implements like rulers or protractors, but with our minds. We need to find a way to measure these shapes using philosophical argument alone.

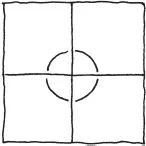
Do you see that in this case what we need to measure are the angles? In order to check that a mosaic pattern like this will work, we need to make sure that at every corner (where the tiles meet) the angles of the polygons add up to a full turn. For instance, the ordinary square tiling works because the angles of a square are quarter turns and it takes four of them to make a full turn.

By the way, I like to measure angles as portions of a full turn instead of using degrees. It seems simpler to me and more natural than using an arbitrary division of a turn into 360 parts (of course you may do as you please). So I’m going to say that a square has a corner angle of 1/4.

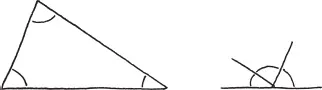
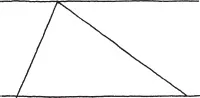
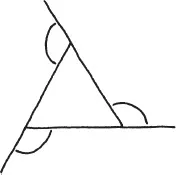
One of the first things people discovered about angles is the surprising fact that for any triangle (no matter what shape) the sum of the angles is always the same, namely a half turn (or 180 degrees if you must be vulgar).

To get a feel for this, you might want to make some paper triangles and cut off their corners. When you join them together, they will always form a straight line. What a beautiful discovery! But how can we really know that it is true?

One way to see it is to view the triangle as being sandwiched between two parallel lines.

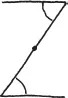
Notice how these lines form Z shapes with the sides of the triangle. (I suppose you might call the one on the right side a backward Z, but it doesn’t really matter.) Now, the thing about Z shapes is that their angles are always equal.

This is because a Z shape is symmetrical: it looks exactly the same if you rotate it a half turn around its center point. That means the angle at the top must be the same as the angle at the bottom. Does that make sense? This is a typical example of a symmetry argument. The invariance of a shape under a certain set of motions allows us to deduce that two or more measurements must be the same.

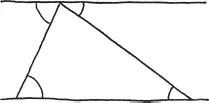
Going back to our triangle sandwich, we see that each angle at the bottom corresponds to an equal angle at the top.

This means that the three angles of the triangle join together at the top to form a straight line. So the three turns add up to a half turn. What a delightful piece of mathematical reasoning!

This is what it means to do mathematics. To make a discovery (by whatever means, including playing around with physical models like paper, string, and rubber bands), and then to explain it in the simplest and most elegant way possible. This is the art of it, and this is why it is so challenging and fun.

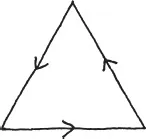
One consequence of this discovery is that if our triangle happens to be equilateral (that is, regular) then its angles are all equal, so they must each be 1/6. Another way to see this is to imagine driving around the perimeter of the triangle.

We make three equal turns to get back to where we started. Since we end up making one complete turn, each of these must be exactly 1/3. Notice that the turns we’ve made are actually the outside angles of the triangle.

Since the inside and outside angles combine to make a half turn, the inside angles must be

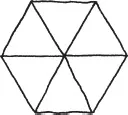
In particular, six of these triangles will fit together at a corner.

Hey, this makes a regular hexagon! So as a bonus, we get that the angles of a regular hexagon must be twice those of the triangle, in other words 1/3. This means that three hexagons fit together perfectly.

So it is possible to have knowledge about these shapes after all. In particular, now we can see why the original mosaic design works.

At each corner of the mosaic, we have a hexagon, two squares, and a triangle. Adding up the angles we get

So it works!

(By the way, if you don’t like doing arithmetic with fractions, you can always avoid it by changing your measuring units. For example, if you’d prefer, we could decide to measure angles in twelfths of a turn, so that the angle of a regular hexagon would simply be 4, a square would have an angle of 3, and a triangle an angle of 2. Then the angles of our shapes would add up to 4 + 3 + 3 + 2 = 12; that is, a full turn.)

I especially love how symmetrical this mosaic pattern is. Each corner has the same exact sequence of shapes around it: hexagon, square, triangle, square. This means that once we’ve checked that the angles fit at one corner, we automatically know that they work at all the other corners. Notice that the pattern can be continued indefinitely so that it covers an entire infinite plane. It makes me wonder what other beautiful mosaic patterns might be out there in mathematical reality?

What are all the different ways to make symmetrical mosaic designs using regular polygons?

Naturally, we’re going to need to know the angles of the various regular polygons. Can you figure out how to measure them?

What are the angles of a regular n-sided polygon?

Can you measure the angles of a regular n-pointed star?

Do the diagonals drawn from one corner of a regular polygon always make equal angles?

While we’re on the subject of pretty patterns made of polygons, I want to show you another of my favorites.

This time we have squares and triangles, but instead of lying ...