From Deep Sea to Laboratory 3

From Tait's Work on the Compressibility of Seawater to Equations-of-State for Liquids

Frederic Aitken, Jean-Numa Foulc

• Publisher: Wiley-ISTE
• Year: 2019
• Print ISBN:
  9781786303769
• eBook ISBN:
  9781119663393
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Oceanography

The scientific expedition of H.M.S. Challenger in the 1870s marks the starting point of physical oceanography. This ship traveled the seas of the globe pursuing a dual objective: to conduct an in-depth study of animal life and to observe the physical properties of ocean waters.

Volume 3 focuses on measurements and modeling of liquid compressibility. Based on the work initiated by the physicist Peter Tait, a detailed presentation of liquid equations-of-state is proposed. The physical interpretation of the parameters of these equations is discussed, leading to a description of the "structure" of liquid media.

From Deep Sea to Laboratory is available in three volumes for curious readers drawn to travel, history and science. Students, researchers and teachers of physics, fluid mechanics and oceanography will find material to deepen their knowledge.

1
The Compressibility of Liquids and Tait’s Equation-of-State

Peter Tait’s high pressure cell

(source: Scientific report of the H.M.S. Challenger, narrative II, 1882)

1.1. Introduction

The temperature-measuring devices used by H.M.S. Challenger scientists have been presented in Volume 2. As pointed out, the high pressures in the seabed caused disruptions and led to errors in temperature measurements. After the return of the expedition, at the request of C.W. Thomson (scientific leader of the Challenger expedition), Peter Tait examined the conditions of use of the devices and carried out a detailed study to evaluate the temperature measurement errors due to the contraction of the solid and liquid components of the thermometers. It is on the basis of this particular study that we develop and present more general notions concerning the measurement of high pressures, the compressibility of liquids and the equations-of-state, with a particular focus on Tait’s equation-of-state in Volume 3. But first, let us look at a practical application using pressure measurement.

Challenger sailors found that ocean depth measurement using a sampling line was not always highly reliable, especially at great depths (see Volume 1, Section 4.4.3). The idea of using a pressure measurement to determine depth therefore appeared to be a relevant alternative. Indeed, a quasi-proportionality relationship exists between these two quantities:

[1.1]

where P* (z) denotes the pressure gradient of the water, at depth z (with P* (0) = 0 ), P is the absolute pressure (P = P_a + P*, P_a being the atmospheric pressure at the sea surface), g is the gravity field and ρ_e (P) is the density of the seawater.

Knowing that the compressibility of seawater is relatively low (at 200 atm, ρ_e decreases by less than 1%), we can consider that ρ_e (P) ≅ Const = ρ_e and that the relationship [1.1] becomes:

[1.2]

The depth is therefore almost proportional to the pressure, with K ≅10 m atm^-1.

To measure pressure, an instrument capable of recording the contraction of a fluid or solid material subjected to pressure must be used. This, of course, presupposes that the response of the stressed material (dependence of its density or relative contraction as a function of the applied pressure) is known. A good knowledge of the compressibility of the materials used to manufacture pressure- (and temperature-) measuring instruments is therefore essential. In Volume 2, section 1.3, we have seen how the contraction of materials (glass, ebonite) affects temperature measurement errors. Peter Guthrie Tait’s work has thus made it possible to better understand the impact of pressure on the reading of Miller-Casella thermometers. In doing so, Tait also realized, on the one hand, that his predecessors’ results on low-pressure fresh water compressibility were very scattered and, on the other hand, that the study of salt solution compressibility was practically non-existent. The study of fresh water compressibility was therefore absolutely necessary because this liquid was widely used in piezometers and the study of the compressibility of salt solutions was also essential to be able to deduce with precision the depth of the sea from a pressure measurement.

Tait’s work after the Challenger’s return allowed him to further develop more general theoretical and experimental studies in the field of fresh water and saline compressibility, the effect of pressure on the maximum density of fresh water, and equations-of-state for liquids. In this chapter, we begin by describing Tait’s approach that led him to write his famous equation-of-state¹. This relationship contains two parameters that change with temperature. In Chapter 2, we continue by comparing Tait’s equation with the equations-of-state of the same period by discussing parameter interpretations. This analysis is extended in Chapter 3 by applications to a few specific fluids that will provide us with the various parameter evolutions. Chapter 4 deals with the adiabatic compressibility module, which allows for modeling supercritical states up to very high pressures.

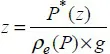
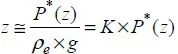
1.2. Concepts of compressibility

Compressibility is a general property of a material that causes anything to reduce its volume under the effect of pressure. This property is characterized by coefficients that can be different depending on the material concerned (gas, liquid or solid). In the case of a liquid (usually a state of matter that cannot withstand static shear stress without flow), the only modulus that can be defined is its modulus of elasticity in volume κ, also called the tangent modulus in volume.

A specific volume V of liquid that is subjected to a hydrostatic pressure variation ΔP = P – P₀ (P is the applied pressure and P₀ the reference pressure) undergoes a volume decrease equal to ΔV; its deformation in volume is: -...

Table of contents

• Cover
• Table of Contents
• Foreword
• Preface
• Notations
• 1 The Compressibility of Liquids and Tait’s Equation-of-State
• 2 Interpretations of the Parameters of Tait’s Equation
• 3 Tait-Tammann-Gibson Equations-of-State
• 4 The Modified Tait Equation
• Conclusion Overview and Contributions of Tait’s Work
• Appendices
• References
• Index
• Summary of Volume 1
• Summary of Volume 2
• End User License Agreement