Induction in Geometry

L.I. Golovina, I. M. Yaglom

• Publisher: Dover Publications
• Year: 2019
• Print ISBN: 9780486838564
• eBook ISBN: 9780486844268
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

Induction in Geometry discusses the application of the method of mathematical induction to the solution of geometric problems, some of which are quite intricate. The book contains 37 examples with detailed solutions and 40 for which only brief hints are provided. Most of the material requires only a background in high school algebra and plane geometry; chapter six assumes some knowledge of solid geometry, and the text occasionally employs formulas from trigonometry. Chapters are self-contained, so readers may omit those for which they are unprepared. 
To provide additional background, this volume incorporates the concise text, The Method of Mathematical Induction. This approach introduces this technique of mathematical proof via many examples from algebra, geometry, and trigonometry, and in greater detail than standard texts. A background in high school algebra will largely suffice; later problems require some knowledge of trigonometry. The combination of solved problems within the text and those left for readers to work on, with solutions provided at the end, makes this volume especially practical for independent study.

1. The Method of Mathematical Induction

1. EXAMPLES OF UNSOUND INDUCTION IN MATHEMATICS

First let us consider two examples of the sort of induction which is inadmissible in mathematics.

EXAMPLE 1. Let

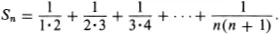
The following equalities are easy to verify:

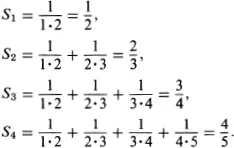
On the basis of these four results, one might conclude that for all natural numbers n it is true that

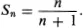
EXAMPLE 2. Next let us consider the trinomial x² + x + 41, first considered by the famous mathematician L. Euler.¹ If we replace x by the number 0 in this trinomial, we obtain the prime number 41. If we replace x by the number 1, we again obtain a prime number, namely 43. If we continue in this manner and replace x by the numbers 2, 3, 4, 5, 6, 7, 8, 9, 10, successively, we obtain in each case a prime number: 47, 53, 61, 71, 83, 97, 113, 131, 151, respectively. On the basis of these results one might conclude that for any nonnegative integer x, the value of the trinomial is a prime number.

Why is the reasoning used in these examples inadmissible in mathematics? In what way is the reasoning invalid?

In both the examples the reasoning employed led us to assert a general statement referring to any n (or any x) on the basis that the statements had been found true for certain particular values of n (or of x). It so happens that the general statement obtained in Example 1 is true, as we shall see below in Example 5; however, the general statement obtained in Example 2 is false. Indeed, while it can be shown that the trinomial x² + x + 41 yields prime numbers for x = 0, 1, 2, 3, ... , 39, for x = 40 the value of the trinomial is seen to be 41², which is a composite number.

Induction has wide applications in mathematics, but it must be used with care or it may lead to erroneous conclusions.

1. MORE EXAMPLES OF UNSOUND INDUCTION

We have encountered in Example 2 a statement which proves to be true in forty instances, but which is not true in general. We shall give two additional examples of statements which are true in some particular instances without being true in general.

EXAMPLE 3. The binomial xⁿ – 1 (where n is a natural number) is of great interest to mathematicians as it is closely related to the geometric problem of dividing a circle into n equal parts. Hence, it is not surprising that this binomial has been studied with great care, with particular attention to the question of resolving it into factors with integral coefficients.

In studying these factorizations for many particular values of n, mathematicians noted that in each of the cases studied, the absolute values of the coefficients of the factors never exceeded the number 1. Thus,

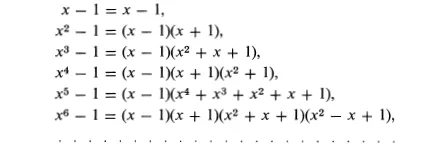
Tables of coefficients were made, and in each case the coefficients had the property mentioned above. Nevertheless, all attempts to prove the statement true for all values of n failed.

The problem was finally solved in 1941 by V. Ivanov with the following result: If n < 105, the binomial xⁿ – 1 has the above property. One of the factors of x¹⁰⁵ – 1, however, is the polynomial

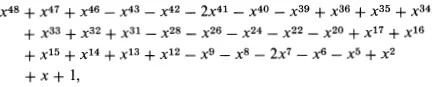
which no longer has this property.

EXAMPLE 4. Into how many parts is space divided by n planes which pass through the same point, but no three of which intersect in the same straight line?

Let us consider the simplest special cases of this problem: One plane divides space into 2 parts. Two planes passing through a common point divide space into 4 parts. Three planes passing through a common point, but having no line in common, divide space into 8 parts.

At first glance it may appear that as the number of planes increases by 1, the number of parts into which they divide space is doubled, so that 4 planes would divide space into 16 parts, 5 planes into 32 parts, and so on; or, in general, that n planes would divide space into 2ⁿ parts.

Actually, this is not the case: 4 planes divide space into 14 parts, 5 planes into 22 parts. In general, n planes divide space into n(n – 1) + 2 parts.¹

These examples illustrate the following simple but important fact: A statement may be true in many special instances and yet not be true in general.

1. THE PRINCIPLE OF MATHEMATICAL INDUCTION

Now the following question arises: Suppose that we have a statement involving natural numbers which we have found to be true in some particular instances. How can we determine whether the statement is true in general; or, to be more specific, how can we determine whether the statement is true for all natural numbers n = 1, 2, 3, ... ?

This question can sometimes be answered by using a special method of reasoning called the method of mathematical induction (complete induction), based on the following principle:

A statement is true for every natural number n if the following conditions are satisfied:

Co...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface to the American Edition
• Contents
• Introduction
• CHAPTER 1. The Method of Mathematical Induction
• CHAPTER 2. Examples and Exercises
• CHAPTER 3. Proofs of Some Theorems of Algebra
• Solutions of Exercises in Chapter 2
• Induction in Geometry
• Preface to the American Edition
• Contents
• Introduction: What Is the Method of Mathematical Induction?
• CHAPTER 1. Computation by Induction
• CHAPTER 2. Proof by Induction
• CHAPTER 3. Construction by Induction
• CHAPTER 4. The Determination of Geometric Loci by Induction
• CHAPTER 5. Definitions by Induction
• CHAPTER 6. Induction on the Number of Dimensions