Deleuze and the History of Mathematics

In Defense of the 'New'

Simon Duffy

• Publisher: Bloomsbury Academic
• Year: 2013
• ISBN:
  9781441179203
• Edition: 1
• Topic: Philosophy
• Subtopic: Philosophy History & Theory

Gilles Deleuze's engagements with mathematics, replete in his work, rely upon the construction of alternative lineages in the history of mathematics, which challenge some of the self imposed limits that regulate the canonical concepts of the discipline. For Deleuze, these challenges provide an opportunity to reconfigure particular philosophical problems - for example, the problem of individuation - and to develop new concepts in response to them. The highly original research presented in this book explores the mathematical construction of Deleuze's philosophy, as well as addressing the undervalued and often neglected question of the mathematical thinkers who influenced his work. In the wake of Alain Badiou's recent and seemingly devastating attack on the way the relation between mathematics and philosophy is configured in Deleuze's work, Simon B.Duffy offers a robust defence of the structure of Deleuze's philosophy and, in particular, the adequacy of the mathematical problems used in its construction. By reconciling Badiou and Deleuze's seemingly incompatible engagements with mathematics, Duffy succeeds in presenting a solid foundation for Deleuze's philosophy, rebuffing the recent challenges against it.

1

Leibniz and the Concept of the Infinitesimal

Gilles Deleuze has gained a lot of respect among historians of philosophy for the rigor and historical integrity of his engagements with figures in the history of philosophy, particularly in those texts that engage with the intricacies of seventeenth century metaphysics and the mathematical developments that contributed to its diversity.¹ One of the aims of these engagements is not only to explicate the detail of the thinker’s thought, but also to recast aspects of their philosophy as developments that contribute to his broader project of constructing a philosophy of difference. Each of these engagements therefore provides as much insight into the developments of Deleuze’s own thought as it does into the detail of the thought of the figure under examination. In order to test this hypothesis, Deleuze’s engagement with Leibniz is singled out for closer scrutiny in this chapter. Much has been made of Deleuze’s Neo-Leibnizianism,² however, very little detailed work has been done on the specific nature of Deleuze’s critique of Leibniz that positions his work within the broader framework of Deleuze’s own philosophical project. This chapter undertakes to redress this oversight by providing an account of the reconstruction of Leibniz’s metaphysics that Deleuze undertakes in The Fold (1993). Deleuze provides a systematic account of the structure of Leibniz’s metaphysics in terms of its mathematical foundations. However, in doing so, Deleuze draws upon not only the mathematics developed by Leibniz—including the law of continuity as reflected in the calculus of infinite series and the infinitesimal calculus—but also developments in mathematics made by a number of Leibniz’s contemporaries and near contemporaries—including Newton’s method of fluxions, the projective geometry that has its roots in the work of Desargues (b. 1591–1661), and the “proto-topology” that appears in the work of Dürer (b. 1471–1528).³ He also draws upon a number of subsequent developments in mathematics, the rudiments of which can be more or less located in Leibniz’s own work—including the theory of functions and singularities, the Weierstrassian theory of analytic continuity, and Poincaré ’s qualitative theory of differential equations. Deleuze then retrospectively maps these developments back onto the structure of Leibniz’s metaphysics. While the Weierstrassian theory of analytic continuity serves to clarify Leibniz’s work, Poincaré ’s qualitative theory of differential equations offers a solution to overcome and extend the limits that Deleuze identifies in Leibniz’s metaphysics. Deleuze brings this elaborate conjunction of material together in order to set up a mathematical idealization of the system that he considers to be implicit in Leibniz’s work. The result is a thoroughly mathematical explication of the structure of Leibniz’s metaphysics. What is provided in this chapter is an exposition of the very mathematical underpinnings of this Deleuzian account of the structure of Leibniz’s metaphysics, which subtends the entire text of The Fold.

Deleuze’s project in The Fold is predominantly oriented by Leibniz’s insistence on the metaphysical importance of mathematical speculation. What this suggests is that mathematics functions as an important heuristic in the development of Leibniz’s metaphysical theories. Deleuze puts this insistence to good use by bringing together the different aspects of Leibniz’s metaphysics with the variety of mathematical themes that run throughout his work, principally the infinitesimal calculus. Those aspects of Leibniz’s metaphysics that Deleuze’s undertakes to clarify in this way, and upon which this chapter will focus, include (1) the definition of a monad; (2) the theory of compossibility; (3) the difference between perception and apperception; (4) the conception of matter and motion; and (5) the range and meaning of the preestablished harmony. However, before providing the details of Deleuze’s reconstruction of the structure of Leibniz’s metaphysics, it will be necessary to give an introduction to Leibniz’s infinitesimal calculus and to some of the other developments in mathematics associated with it.

Leibniz’s law of continuity and the infinitesimal calculus

Leibniz was both a philosopher and mathematician. As a mathematician, he made a number of innovative contributions to developments in mathematics. Chief among these was his infinitesimal analysis, which encompassed the investigation of infinite sequences and series, the study of algebraic and transcendental curves⁴ and the operations of differentiation and integration upon them, and the solution of differential equations: integration and differentiation being the two fundamental operations of the infinitesimal calculus that he developed.

Leibniz applied the calculus primarily to problems about curves and the calculus of finite sequences, which had been used since antiquity to approximate the curve by a polygon in the Archimedean approach to geometrical problems by means of the method of exhaustion. In his early exploration of mathematics, Leibniz applied the theory of number sequences to the study of curves and showed that the differences and sums in number sequences correspond to tangents and quadratures, respectively, and he developed the conception of the infinitesimal calculus by supposing the differences between the terms of these sequences to be infinitely small (See Bos 1974, 13). One of the keys to the calculus that Leibniz emphasized was to conceive the curve as an infinitangular polygon: ⁵

I feel that this method and others in use up till now can all be deduced from a general principle which I use in measuring curvilinear figures, that a curvilinear figure must be considered to be the same as a polygon with infinitely many sides. (Leibniz 1962, V, 126)

Leibniz based his proofs for the infinitangular polygon on a law of continuity, which he formulated as follows: “In any supposed transition, ending in any terminus, it is permissible to institute a general reasoning, in which the final terminus may also be included” (Leibniz 1920, 147). Leibniz also thought the following to be a requirement for continuity:

When the difference between two instances in a given series, or in whatever is presupposed, can be diminished until it becomes smaller than any given quantity whatever, the corresponding difference in what is sought, or what results, must of necessity also be diminished or become less than any given quantity whatever. (Leibniz 1969, 351)

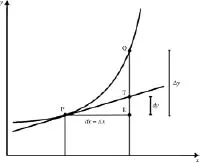
Leibniz used the adjective continuous for a variable ranging over an infinite sequence of values. In the infinite continuation of the polygon, its sides become infinitely small and its angles infinitely many. The infinitangular polygon is considered to coincide with the curve, the infinitely small sides of which, if prolonged, would form tangents to the curve, where a tangent is a straight line that touches a circle or curve at only one point. Leibniz applied the law of continuity to the tangents of curves as follows: he took the tangent to be continuous with or as the limiting case (“terminus”) of the secant. To find a tangent is to draw a straight line joining two points of the curve—the secant—which are separated by an infinitely small distance or vanishing difference, which he called “a differential” (See Leibniz 1962, V, 223). The Leibnizian infinitesimal calculus was built upon the concept of the differential. The differential, dx, is the difference in x values between two consecutive values of the variable at P (See Figure 1.1), and the tangent is the line joining such points.

The differential relation, i.e. the quotient between two differentials of the type dy/dx, serves in the determination of the gradient of the tangent to the circle or curve. The gradient of a tangent indicates the slope or rate of change of the curve at that point, i.e. the rate at which the curve changes on the y-axis relative to the x-axis. Leibniz thought of the dy and dx in dy/dx as “infinitesimal” quantities. Thus dx was an infinitely small nonzero increment in x and dy was an infinitely small nonzero increment in y.

Figure 1.1 The tangent to the curve at P.

Leibniz brings together the definition of the differential as it operates in the calculus of infinite series, in regard to the infinitangular polygon, and the infinitesimal calculus, in regard to the determination of tangents to curves, as follows:

Here dx means the element, i.e. the (instantaneous) increment or decrement, of the (continually) increasing quantity x. It is also called difference, namely the difference between two proximate x’s which differ by an element (or by an inassignable), the one originating from the other, as the other increases or decreases (momentaneously). (Leibniz 1962, VII, 223)

The differential can therefore be understood on the one hand, in relation to the calculus of infinite series, as the infinitesimal difference between consecutive values of a continuously diminishing quantity, and on the other, in relation to the infinitesimal calculus, as an infinitesimal quantity. The operation of the differential in the latter actually demonstrates the operation of the differential in the former, because the operation of the differential in the infinitesimal calculus in the determination of tangents to curves demonstrates that the infinitely small sides of the infinitangular polygon are continuous with the curve. Carl Boyer, in The history of the calculus and its conceptual development, refers to this early form of the infinitesimal calculus as the infinitesimal calculus from “the differential point of view” (1959, 12).

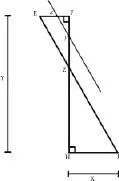
In one of his early mathematical manuscripts entitled “Justification of the Infinitesimal Calculus by That of Ordinary Algebra,” Leibniz offers an account of the infinitesimal calculus in relation to a particular geometrical problem that is solved using ordinary algebra (Leibniz 1969, 545–6). An outline of the demonstration that Leibniz gives is as follows:⁶

Figure 1.2 Leibniz’s example of the infinitesimal calculus using ordinary algebra.

Since the two right triangles, ZFE and ZHJ, that meet at their apex, point Z, are similar, it follows that the ratio y/x is equal to (Y–y)/X. As the straight line EJ approaches point F, maintaining the same angle at the variable point Z, the lengths of the straight lines FZ and FE, or y and x, steadily diminish, yet the ratio of y to x remains constant. When the straight line EJ passes through F, the points E and Z coincide with F, and the straight lines, y and x, vanish. Yet y and x will not be absolutely nothing since they preserve the ratio of ZH to HJ, represented by the proportion (Y–y)/X, which in this case reduces to Y/X, and obviously does not equal zero. The relation y/x continues to exist even though the terms have vanished since the relation is determinable as equal to Y/X. In this algebraic calculus, the vanished lines x and y are not taken for zeros since they still have an algebraic relation to each other. “And so,” Leibniz argues, “they are treated as infinitesimals, exactly as one of the elements which . . . differential calculus recognizes in the ordinates of curves for momentary increments and decrements” (Leibniz 1969, 545). That is, the vanished lines x and y are determinable in relation to each other only insofar as they can be replaced by the infinitesimals dy and dx, by making the supposition that the ratio y/x is equal to the ratio of the infinitesimals, dy/dx. When the relation continues even though the terms of the relation have disappeared, a continuity has been constructed by algebraic means that is instructive of the operations of the infinitesimal calculus.

What Leibniz demonstrates in this example are the conditions according to which any unique triangle can be considered as the extreme case of two similar triangles opposed at the vertex.⁷ Deleuze argues that, in the case of a figure in which there is only one triangle, the other triangle is there, but it is only there “virtually” (Sem. 22 Apr 1980). The virtual triangle has not simply disappeared, but rather it has become unassignable, all the while remaining completely determined. The hypotenuse of the virtual triangle can be mapped as a side of the infinitangular polygon, which, if prolonged, forms a tangent line to the curve. There is therefore continuity from the polygon to the curve, just as there is continuity from two similar triangles opposed at the vertex to a single triangle. Hence this relation is fundamental for the application of differentials to problems about tangents.

In the first published account of the calculus (Leibniz 1684), Leibniz defines the ratio of infinitesimals as the quotient of first-order differentials, or the associated differential relation. He says that “the differential dx of the abscissa x is an arbitrary quantity, and that the differential dy of the ordinate y is defined as the quantity which is to dx as the ratio of the ordinate to the subtangent” (Boyer 1959, 210). (See Figure 1.1) Leibniz considers differentials to be the fundamental concepts of the infinitesimal calculus, the differential relation being defined in terms of these differentials.

Newton’s method of fluxions and infinite series

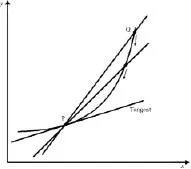
Newton began thinking of the rate of change, or fluxion, of continuously varying quantities, which he called fluents such as lengths, areas, volumes, distances, and temperatures, in 1665, which predates Leibniz by about ten years. Newton regards his variables as generated by the continuous motion of points, lines, and planes, and offers an account of the fundamental problem of the calculus as follows: “Given a relation between two fluents, find the relation between their fluxions, and conversely” (Newton 1736). Newton thinks of the two variables whose relation is given as changing with time, and, although he does point out that this is useful rather than necessary, it remains a defining feature of his approach and is exemplified in the geometrical reasoning about limits, which Newton was the first to come up with.⁸ Put simply, to determine the tangent to a curve at a specified point, a second point on the curve is selected, and the gradient of the line that runs through both of these points is calculated. As the second point approaches the point of tangency, the gradient of the line between the two points approaches the gradient of the tangent. The gradient of the tangent is, therefore, the limit of the gradient of the line between the two points as the points become increasingly close to one another (See Figure 1.3).

He conceptualized the tangent geometrically, as the limit of a sequence of lines between two points, P and Q, on a curve, which is a secant. As the distance between the points approached zero, the secants became progressively smaller, however, they always retained “a real length.” The secant therefore approached the tangent without reaching it. When this distance “got arbitrarily small (but remained a real number)” (Lakoff and Núñez 2000, 224), it was considered insignificant for practical purposes, and was ignored. What is different in Leibniz’s method is that he “hypothesized infinitely small numbers—infinitesimals—to designate the size of infinitely small intervals” (Lakoff and Núñez 2000, 224). (See Figure 1.1) For Newton, on the contrary, these intervals remained only small, and therefore real. When performing calculations, however, both approaches yielded the same results. But they differed ontologically, because Leibniz had hypothesized a new kind of number, a number Newton did not need, since “his secants always had a real length, while Leibniz’s had an infinitesimal length” (Lakoff and Núñez 2000, 224). Leibniz’s symbolism also treats quantities independently of their genesis, rather than as the product of an explicit functional relation.

Figure 1.3 Newton’s geometrical reasoning about the gradient of a tangent as a limit.

Both Newton and Leibniz are credited with developing the calculus as a new and general method, and with having appreciated that the operations in the new analysis are applicable to infinite series as well as to finite algebraic expressions. However, neither of them clearly understood nor rigorously defined their fundamental concepts. Newton thought his underlying methods were natural extensions of pure geometry, while Leibniz felt that the ultimate justification of his procedures lay in their effectiveness. For the next two hundred years, various attempts were made to find a rigorous arithmetic foundation for the calculus: one that relied neither on the mathematical intuition of geometry, with its tangents and secants, which was perceived as imprecise because its conception of limits was not properly understood, nor on the vagaries of the infinitesimal, which could not be justified either from the point of view of classical algebra or from the point of view of arithmetic, and therefore made many mathematicians wary, so much so that they refused the hypothesis outright despite the fact that Leibniz “could do calculus using arithmetic without geometry—by using infinitesimal numbers” (Lakoff and Núñez 2000, 224–5).

The emergence of the concept of the function

Seventeenth century analysis was a corpus of analytical tools for the study of geometric objects, the most fundamental object of which, thanks to the development of a curvilinear mathematical physics by Christiaan Huygens (b. 1629–1695), was the curve, or curvilinear figures generally, which were und...