Stochastic Geometry

Likelihood and Computation

Wilfrid S. Kendall

• Publisher: Routledge
• Year: 2019
• ISBN:
  9781351413718
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

Stochastic geometry involves the study of random geometric structures, and blends geometric, probabilistic, and statistical methods to provide powerful techniques for modeling and analysis. Recent developments in computational statistical analysis, particularly Markov chain Monte Carlo, have enormously extended the range of feasible applications. Stochastic Geometry: Likelihood and Computation provides a coordinated collection of chapters on important aspects of the rapidly developing field of stochastic geometry, including:
o a "crash-course" introduction to key stochastic geometry themes
o considerations of geometric sampling bias issues
o tesselations
o shape
o random sets
o image analysis
o spectacular advances in likelihood-based inference now available to stochastic geometry through the techniques of Markov chain Monte Carlo

CHAPTER 1

A crash course in stochastic geometry

Adrian J. Baddeley

University of Western Australia

This chapter aims to give the reader a rapid introduction to the main ideas of stochastic geometry. It is not a literature review but rather a very selective presentation of some of the key points.

1.1 Introduction

Stochastic geometry is the study of random processes whose outcomes are geometrical objects or spatial patterns, that is, random subsets of ℝ^d or some other given space. It has applications to digital image analysis, spatial statistics and stereology, and connections with many areas of probability and statistics. One of its most appealing, direct applications is to the analysis of spatial patterns, such as those shown in Figures 1.1 and 1.2.

Figure 1.1 Left: California redwood saplings (circles) in a 23 m square, extracted by Ripley (1981) from Strauss (1975). Right: copper deposits (dots) and geological faults (line segments) in a 100×200 km² region, from Berman (1986) Data reproduced by kind permission of Prof. B.D. Ripley and Dr. M. Berman.

Figure 1.2 Heather vegetation (black) and uncovered soil (white) in a 20×10 m² sampling area, from a study by Diggle (1983). Data reproduced by kind permission of Prof. P.J. Diggle.

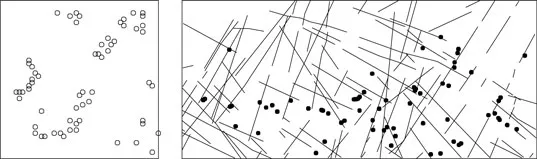
The earliest examples of random geometry were parlour games in which a coin or stick is thrown haphazardly onto a flat surface, and the gamble depends on the final location of the object thrown. From this developed a theory of geometrical probability, concerned mainly with problems in which rigid geometrical figures are randomly positioned in the plane according to an appropriate uniform distribution or uniform Poisson process. This is capable of modelling patterns such as those in Figure 1.1. This classical theory, closely related to integral geometry, reveals many fascinating connections between convex geometry and probability. See Kendall and Moran (1963), Santaló (1976), Schneider and Weil (1992), Solomon (1978).

Modern stochastic geometry handles random subsets of arbitrary form, for example, the zero set of a random function, or a randomly-generated fractal. It also deals with very general classes of probability models, such as stationary random sets in ℝ^d. These are capable of modelling spatial patterns such as that in Figure 1.2. See Harding and Kendall (1974), Matheron (1975), Mecke et al. (1990), Stoyan et al. (1987), Stoyan and Stoyan (1992), Weil and Wieacker (1993) and Cressie (1991, cha...

Table of contents

• Cover
• Title Page
• Copyright Page
• Table of Contents
• Contributors
• Preface
• 1 Crash course in stochastic geometry
• 2 Sampling and censoring
• 3 Likelihood inference for spatial point processes
• 4 Markov chain Monte Carlo and spatial point processes
• 5 Topics in Voronoi and Johnson-Mehl tessellations
• 6 Mathematical morphology
• 7 Random closed sets
• 8 General shape and registration analysis
• 9 Nash inequalities
• Index