Uncovering Student Thinking in Mathematics

25 Formative Assessment Probes

Cheryl M. Rose, Leslie Minton, Carolyn Arline, Cheryl Rose Tobey, Leslie G. Minton, Carolyn B. Arline

• Publisher: Corwin
• Year: 2006
• Print ISBN: 9781412940375, 9781412940368
• eBook ISBN: 9781483334103
• Edition: 1
• Topic: Education
• Subtopic: Teaching Mathematics

"Uncovering Student Thinking in Mathematics shows us ways to listen and observe children and their mathematical understandings so we can find better ways to help them take their next learning steps. This book is a gift to educators who ?seek to understand before being understood.?"
—From the Foreword by Anne Davies

"A fresh and unique resource for mathematics teachers who recognize the importance of carefully establishing the starting points of instruction in terms of what students already know. The collection of assessment probes is inventive, engaging for students, and invaluable for teachers."
—Richard H. Audet, Associate Professor, Roger Williams University

Use formative assessment probes to take the guesswork out of mathematics instruction and improve learning!

Students learn at varying rates, and if a misconception in mathematics develops early, it may be carried from year to year and obstruct a student?s progress. To identify fallacies in students? preconceived ideas, Uncovering Student Thinking in Mathematics offers educators a powerful diagnostic technique in the form of field-tested assessment probes—brief, easily administered activities to determine students? thinking on core mathematical concepts.

Designed to question students? conceptual knowledge and reveal common understandings and misunderstandings, the probes generate targeted information for modifying mathematics instruction, allowing teachers to build on students? existing knowledge and individually address their identified difficulties.

Linked to National Council of Teachers of Mathematics standards, this invaluable handbook assists educators with:

• 25 ready-to-use mathematical probes
• Teacher guides for implementing each probe at any grade level
• Examples of typical obstacles and faulty thinking demonstrated by students

This rich resource combines standards, educational research findings, and practical craft knowledge to help teachers deliver informed instruction that strengthens all students? learning and achievement in mathematics.

1

---

Mathematics
Assessment Probes

To differentiate instruction effectively, teachers need diagnostic assessment strategies to gauge their students’ prior knowledge and uncover their misunderstandings. By accurately identifying and addressing misunderstandings, teachers prevent their students from becoming frustrated and disenchanted with mathematics, which can reinforce the student preconception that “some people don't have the ability to do math.” Diagnostic strategies also allow for instruction that builds on individual students’ existing understandings while addressing their identified difficulties. The Mathematics Assessment Probes in this book allow teachers to target specific areas of difficulty as identified in research on student learning. Targeting specific areas of difficulty—for example, the transition from reasoning about whole numbers to understanding numbers that are expressed in relationship to other numbers (decimals and fractions)—focuses diagnostic assessment effectively (National Research Council, 2005, p. 310).

Mathematics Assessment Probes represent one approach to diagnostic assessment. They typically include a prompt or question and a series of responses. The probes specifically elicit prior understandings and commonly held misconceptions that may or may not have been uncovered during an instructional unit. This elicitation allows teachers to make instructional choices based on the specific needs of students. Examples of commonly held misconceptions elicited by a Mathematics Assessment Probe include ideas such as multiplication makes bigger and the larger the denominator, the larger the fraction.

It is important to make the distinction between what we might call a silly mistake and a more fundamental one, which may be the product of a deeprooted misunderstanding. It is not uncommon for different students to display the same misunderstanding every year. Being aware of and eliciting common misunderstandings and drawing students’ attention to them can be a valuable teaching technique (Griffin & Madgwick, 2005).

The process of diagnosing student understandings and misunderstandings and making instructional decisions based on that information is the key to increasing students’ mathematical knowledge. To use the Mathematics Assessment Probes for this purpose, teachers need to:

• Determine a question
• Use a probe to examine student understandings and misunderstandings
• Use links to cognitive research to drive next steps in instruction
• Implement the instructional unit or activity
• Determine the impact on learning by asking an additional question

The above process is described in detail in this chapter. The Teachers’ Notes that accompany each of the Mathematics Assessment Probes in Chapters 3 through 5 include information on research findings and instructional implications relevant to the individual probe.

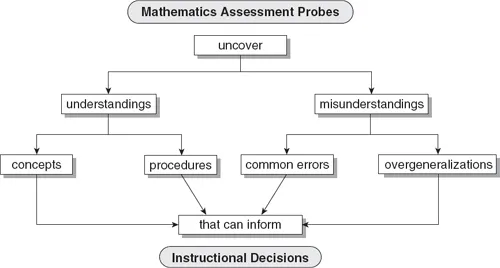
WHAT TYPES OF UNDERSTANDINGS AND MISUNDERSTANDINGS DOES A MATHEMATICS ASSESSMENT PROBE UNCOVER?

Developing understanding in mathematics is an important but difficult goal. Being aware of student difficulties and the sources of the difficulties, and designing instruction to diminish them, are important steps in achieving this goal. (Yetkin, 2003)

The Mathematics Assessment Probes are designed to uncover student understandings and misunderstandings; the results are used to inform instruction rather than make evaluative decisions. As shown in Figure 1.1, the understandings include both conceptual and procedural knowledge and misunderstandings are classified as common errors or overgeneralizations. Each of these is described in more detail below.

Understandings: Conceptual and Procedural Knowledge

Research has solidly established the importance of conceptual understanding in becoming proficient in a subject. When students understand mathematics, they are able to use their knowledge flexibly. They combine factual knowledge, procedural facility, and conceptual understanding in powerful ways (National Council of Teachers of Mathematics [NCTM], 2000).

Conceptual Understanding

Students demonstrate conceptual understanding in mathematics when they:

• Recognize, label, and generate examples and nonexamples of concepts
• Use and interrelate models, diagrams, manipulatives, and so on
• Know and apply facts and definitions
• Compare, contrast, and integrate concepts and principles
• Recognize, interpret, and apply signs, symbols, and terms
• Interpret assumptions and relationships in mathematical settings

Figure 1.1 Mathematics Assessment Probes

---

Procedural Knowledge

Students demonstrate procedural knowledge in mathematics when they:

• Select and apply appropriate procedures
• Verify or justify a procedure using concrete models or symbolic methods
• Extend or modify procedures to deal with factors in problem settings
• Use numerical algorithms
• Read and produce graphs and tables
• Execute geometric constructions
• Perform noncomputational skills such as rounding and ordering (U.S. Department of Education, 2003, Chapter 4)

The relationship between understanding concepts and being proficient with procedures is complex. The following description gives an example of how the Mathematics Assessment Probes elicit conceptual or procedural understanding.

The Volume of the Box probe (see Figure 1.2) is designed to elicit whether students understand the formula numerically and quantitatively (NCTM, 2003, p. 101). Students who correctly determine the volume of the first problem, yet choose C. Not enough information for the second problem may be able to apply the volume formula, V = lwh, when given a length, width, and height but lack the ability to apply the formula to a varied representation of the concept. The following student responses to “Explain Your Reasoning” are indicative of conceptual understanding of the formula:

• “Volume is the area of the base times the height. If you flip this box, the 24 is the base and 4 is the height so 24 cm² × 4 cm is 96 cm³.”
  Figure 1.2 Volume of a Box Probe
  

  ---

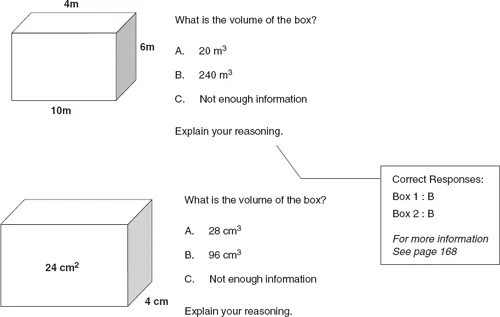
• “You already have some of the information needed. If you rearrange l × w × h to fit the information given, you would have (l × h) × w. You are given that l × h is 24 cm² and (24 cm²) (4 cm) = 96 cm³.”

Misunderstandings: Common Errors and Overgeneralizations

In “Hispanic and Anglo Students’ Misconceptions in Mathematics,” Jose Mestre summarizes cognitive research as follows:

Students do not come to the classroom as “blank slates” (Resnick, 1983). Instead, they come with theories constructed from their everyday experiences. They have actively constructed these theories, an activity crucial to all successful learning. Some of the theories that students use to make sense of the world are, however, incomplete halftruths (Mestre, 1987). They are misconceptions.

Misconceptions are a problem for two reasons. First, they interfere with learning when students use them to interpret new experiences. Second, students are emotionally and intellectually attached to their misconceptions because they have actively constructed them. Hence, students give up their misconceptions, which can have such a harmful effect on learning, only with great reluctance.

For the purposes of this book, these misunderstandings or misconceptions will be categorized into common errors and overgeneralizations. Each of these categories of misunderstandings is described in more detail.

Common Error Patterns

Common error patterns refer to systematic uses of inaccurate/inefficient procedures or strategies. Typically, this type of error pattern indicates nonunderstanding of an important math concept (University of Kansas, 2005). Examples of common error patterns include consistent misuse of a tool or steps of an algorithm, such as an inaccurate procedure for computing or the misreading of a measurement device. The following description gives an example of how the Mathematics Assessment Probes elicit common error patterns.

The How Long Is the Pencil? probe (see Figure 1.3) is designed to elicit understanding of zero-point. “A significant minority of older children (e.g., fifth grade) respond ...

Table of contents

• Cover Page
• Dedication
• Title
• Copyright
• Contents
• Foreword by Anne Davies
• Preface
• Acknowledgments
• About the Authors
• Chapter 1: Mathematics Assessment Probes
• Chapter 2: Instructional Implications
• Chapter 3: Number and Operations Assessment Probes
• Chapter 4: Algebra, Data Analysis, and Probability Assessment Probes
• Chapter 5: Geometry and Measurement Assessment Probes
• Resource A: Note Template
• References
• Index