Game Theory

A Nontechnical Introduction

Morton D. Davis

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486296722
• eBook ISBN: 9780486135151
• Topic: Mathematics
• Subtopic: Teaching Mathematics
• Index: Mathematics

"A lucid and penetrating development of game theory that will appeal to the intuition . . . a most valuable contribution." — Douglas R. Hofstadter, author of Gödel, Escher, Bach
The foundations of game theory were laid by John von Neumann, who in 1928 proved the basic minimax theorem, and with the 1944 publication of the Theory of Games and Economic Behavior, the field was established. Since then, game theory has become an enormously important discipline because of its novel mathematical properties and its many applications to social, economic, and political problems.
Game theory has been used to make investment decisions, pick jurors, commit tanks to battle, allocate business expenses equitably — even to measure a senator's power, among many other uses. In this revised edition of his highly regarded work, Morton Davis begins with an overview of game theory, then discusses the two-person zero-sum game with equilibrium points; the general, two-person zero-sum game; utility theory; the two-person, non-zero-sum game; and the n-person game.
A number of problems are posed at the start of each chapter and readers are given a chance to solve them before moving on. (Unlike most mathematical problems, many problems in game theory are easily understood by the lay reader.) At the end of the chapter, where solutions are discussed, readers can compare their "common sense" solutions with those of the author. Brimming with applications to an enormous variety of everyday situations, this book offers readers a fascinating, accessible introduction to one of the most fruitful and interesting intellectual systems of our time.

1

An Overview

The theory of games is a theory of decision making. It considers how one should make decisions and, to a lesser extent, how one does make them. You make a number of decisions every day. Some involve deep thought, while others are almost automatic. Your decisions are linked to your goals—if you know the consequences of each of your options, the solution is easy. Decide where you want to be and choose the path that takes you there. When you enter an elevator with a particular floor in mind (your goal), you push the button (one of your choices) that corresponds to your floor. Building a bridge involves more complex decisions but, to a competent engineer, is no different in principle. The engineer calculates the greatest load the bridge is expected to bear and designs a bridge to withstand it.

When chance plays a role, however, decisions are harder to make. A travel agency may want to give its customers prompt service and yet avoid excessive telephone bills. But since the agency doesn’t know what future demands will be, it doesn’t know how many phones to install. By using past experience and applying the laws of probability, a balance can be struck between losses from excessive phone bills and defecting customers.

Game theory was designed as a decision-making tool to be used in more complex situations, situations in which chance and your choice are not the only factors operating. These are the situations that will concern us from now on. Let’s look at a few such examples to clarify what I am saying and postpone our analysis of these kinds of problems to the later chapters.

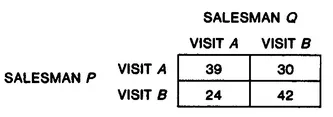
Companies A and B intend to buy 30 and 24 typewriters, respectively. Salesman P represents the company that currently supplies them both; Q represents a competitor. Each has time to give one sales talk at either company A or B. If they visit the same company, they divide the sales at that company equally but P makes all the sales to the other company. If they visit different companies, each makes all the sales at the company visited. In figure 1.1 the alternatives for salesman Q are represented by columns and the alternatives for P are represented by rows. The entry corresponding to each pair of alternatives represents P’s total sales (since there are 54 typewriter sales in all, Q’s total sales can be deduced from P’s sales).

Figure 1.1

If Q and P both visit A, for example, we find the entry where column “Visit A” meets the row “Visit A” is 39. P gets half the sales at A and all the sales at B, which is 15 + 24 = 39. It is understood that ,Q had 15 sales since the total number of sales is 54.

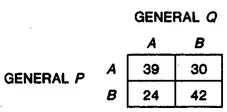
Generals P and Q each want control of oil deposits that P now controls. Thirty acres are located at A and 24 are located at B. Q has enough strength to invade only one location and P has enough strength to defend only one. Both forces are equally matched, so if P and Q go to the same place there will be a standoff; each gets half the acreage there while P retains control of the other location. If P and Q choose different locations, each army will control all the acreage at its own location.

Figure 1.2 indicates the total acreage that P will control.

Figure 1.2

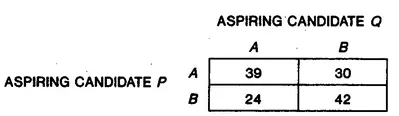
On the last day of a political convention, aspiring candidates P and Q will meet delegates from either states A or B. P is the current favorite, so if both candidates visit the same state, each will get half the delegates of that state and P will get all the delegates of the other one; if they visit different states, each will get the delegates of the state visited. If A and B have 30 and 24 delegates, respectively, the possible outcomes are reflected in figure 1.3.

Figure 1.3

Although these three situations differ—one involves business competition, another military conflict, and the third a political campaign—they all reduce to a single problem involving the theory of games. They differ from the problems described earlier—building a bridge and installing telephones—in one essential respect: While decision makers are trying to manipulate their environment, their environment is trying to manipulate them. A store owner who lowers her price to gain a larger share of the market must know that her competitors will react in kind. A thief who robs banks rather than newsstands (because that’s where the money is) must be aware that the police will be asking themselves “Where would I go if I were a thief?” and act accordingly. The bridge under construction, on the other hand, has no feelings about its own safety, and the travel agency’s customers were not trying to embarrass it by calling too frequently or not calling it frequently enough.

A player involved in a game with other decision-making players is in the same position as the scientist who wanted to study a monkey’s behavior. After he placed the monkey in a room and gave it time to get acclimated, he looked through the observation slot—and saw the monkey’s eyeball looking back at him.

In the rest of this book I will talk about certain situations that I will call games. In a game there will be players (at least two), and each will pick a strategy (make a decision). As a result of this joint choice—and possibly chance, a disinterested player—the result will be a reward or punishment for each player: the payoff. Because everyone’s strategy affects the outcome, a player must worry about what everyone else does and knows that everyone else is worrying about him or her.

The words “strategy,” “player,” and “payoff” have roughly the same meaning here as they do in everyday language. A player, a participant in the game, need not be a single person. If each member of a group has exactly the same feelings about how the game should turn out, the members may be considered a single player. So a “player” may be a corporation, a county, or a football team.

A strategy in game theory is a complete plan of action that describes what a player will do under all possible circumstances. In ordinary usage a strategy is considered to be something clever, but nothing like that is intended here. There are poor strategies, just as there are good strategies. In the three examples depicted in figures 1.1 to 1.3, each player had two simple strategies—A and B—but in real games strategies may be so complex that they can’t be written out explicitly. Also, in some real games it might seem convenient to think of a player as using several different strategies. Competing automobile companies that fix their prices every year and chess players who rethink their position after each move are two examples. But in principle you can imagine that all these decisions are merged into one to form a single strategy, and from the point of view of the theorist this is more convenient.

A complete strategy in chess, then, would start something like this: “On my first move I will move to position A. If he then moves to B, then I’ll move to B’; if he then moves to C, I’ll move to C’; if he ... If after I move to A, he moves to B, I move to B’. If he then moves to Q, I’ll move to Q’...” It is almost impossible to describe a complete strategy in detail in any real game one actually plays, and even in such a simple game as tick-tack-toe, which is played by very young children, the task is formidable. But the practical problem of writing out an entire strategy in detail shouldn’t stop us from making use of the concept any more than our inability to multiply all the numbers from I to 1,000 shouldn’t stop us from writing a formula in which this product appears.

This distinction between theory and practice is very important; the difference becomes clear if you compare a chess player’s attitude toward the game of chess with that of the game theorist. Chess has been around for many centuries, and no human being or computer has come close to mastering it. In films and cartoons the bearded chess player is often used to symbolize profound thought, and, in fact, the chess player finds the game profound and subtle. To the game theorist, however, the game is trivial. This seems an absurd position, since game theorists are not even particularly good chess players.

The apparent paradox is easily resolved, however; chess, complex as it is, is finite, so, in principle, every position on the board is either (a) a win for white, (b) a draw, or (c) a win for black. Given enough time, you could start from the end of the game and work forward labeling every position that can possibly arise in the game as a win, loss, or draw and finally determine whether the game itself is a win, loss, or draw. (This technique would also indicate how to enforce the win or draw.) In practice the task is hopeless, of course, so from the chess player’s point of view the game is as deep as he or she believes it to be.

There is also a difference in the way we will be analyzing our “games” and the way experts analyze parlor games. If a player in a game like chess has a winning strategy, we assume he will use it; if a player is in great difficulty and needs to adopt a very subtle defense to draw, we assume she will find it. In short, we assume players always do their best.

In real life, it may make an enormous difference how you play even if you are backing a lost cause. Against an ideal player you may be defeated, but against a real person it is well known that certain strategies induce errors. Emanuel Lasker, world chess champion for many years, felt that psychology plays a very important role in the game. He often adopted a slightly inferior opening, which initially gave him a slight disadvantage, in order to disconcert his opponent. And a Russian handbook on championship chess suggests that a player should try to force an opponent into an early commitment, even if by doing so the first player obtains a slightly inferior position. In the children’s game of tick-tack-toe, the outcome will always be a draw if there is correct play on both sides, but there is a pragmatic argument for making the first move in the corner: there is only one answer to the corner move that preserves the draw, and that is a move in the center. Any other first move allows at least four adequate replies. So, in a sense, the corner move is strongest, but it is a sense that the game theorist does not recognize. Game theorists do not speak of “slightly unfavorable positions” or “commitments” or “attacks,” premature or otherwise. They are incompetent to deal with the game on these terms, and these terms are superfluous to their theory. In short, game theorists, do not attempt to exploit their opponent’s folly.

Since it takes no great insight to recognize the existence of folly in this world, and since the game theorist purports to be influenced by the world, why this puristic attitude? The answer is simply this: it is much easier to recognize the existence of error than to fashion a general, systematic theory that will allow you to exploit it. So the study of tricks is left to the experts in each particular game; game theorists make the pessimistic, and often imperfect, assumption that their opponents will play flawlessly.

Games like chess, checkers, tick-tack-toe, and the Japanese game of Go are called games of perfect information because everyone knows exactly what is going on at all times. These games offer few conceptual problems, and they won’t be discussed here. In games like poker and bridge the players are, to some extent, kept in the dark, and in this sense the games are more complex. Even as trivial a ga...

Table of contents

• DOVER BOOKS ON MATHEMATICS
• Title Page
• Copyright Page
• Dedication
• Table of Contents
• Foreword to the First Edition
• Author’s Introduction
• Acknowledgements
• 1 - An Overview
• 2 - The Two-Person, Zero-Sum Game with Equilibrium Points
• 3 - The General, Two-Person, Zero-Sum Game
• 4 - Utility Theory
• 5 - The Two-Person, Non-Zero-Sum Game
• 6 - The n-Person Game
• Bibliography
• A CATALOG OF SELECTED DOVER BOOKS IN ALL FIELDS OF INTEREST
• DOVER BOOKS ON SCIENCE