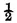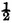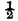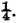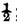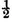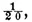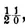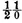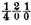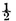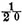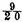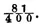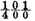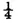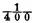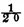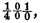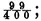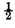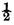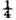A Philosophical Essay on Probabilities

Pierre-Simon Laplace

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486288758
• eBook ISBN: 9780486170343
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

A classic of science, this famous essay by "the Newton of France" introduces lay readers to the concepts and uses of probability theory. It is of especial interest today as an application of mathematical techniques to problems in social and biological sciences.
Generally recognized as the founder of the modern phase of probability theory, Laplace here applies the principles and general results of his theory "to the most important questions of life, which are, in effect, for the most part, problems in probability." Thus, without the use of higher mathematics, he demonstrates the application of probability to games of chance, physics, reliability. of witnesses, astronomy, insurance, democratic government and many other areas.
General readers will find it an exhilarating experience to follow Laplace's nontechnical application of mathematical techniques to the appraisal, solution and/or prediction of the outcome of many types of problems. Skilled mathematicians, too, will enjoy and benefit from seeing how one of the immortals of science expressed so many complex ideas in such simple terms.

PART II.

APPLICATIONS OF THE CALCULUS OF PROBABILITIES.

CHAPTER VI.

GAMES OF CHANCE

THE combinations which games present were the object of the first investigations of probabilities. In an infinite variety of these combinations many of them lend themselves readily to calculus; others require more difficult calculi; and the difficulties increasing in the measure that the combinations become more complicated, the desire to surmount them and curiosity have excited geometricians to perfect more and more this kind of analysis. It has been seen already that the benefits of a lottery are easily determined by the theory of combinations. But it is more difficult to know in how many draws one can bet one against one, for example that all the numbers will be drawn, n being the number of numbers, r that of the numbers drawn at each draw, and i the unknown number of draws. The expression of the probability of drawing all the numbers depends upon the nth finite difference of the i power of a product of r consecutive numbers. When the number n is considerable the search for the value of i which renders this probability equal to

becomes impossible at least unless this difference is converted into a very converging series. This is easily done by the method here below indicated by the approximations of functions of very large numbers. It is found thus since the lottery is composed of ten thousand numbers, one of which is drawn at each draw, that there is a disadvantage in betting one against one that all the numbers will be drawn in 95767 draws and an advantage in making the same bet for 95768 draws. In the lottery of France this bet is disadvantageous for 85 draws and advantageous for 86 draws.

Let us consider again two players, A and B, playing together at heads and tails in such a manner that at each throw if heads turns up A gives one counter to B, who gives him one if tails turns up; the number of counters of B is limited, while that of A is unlimited, and the game is to end only when B shall have no more counters. We ask in how many throws one should bet one to one that the game will end. The expression of the probability that the game will end in an i number of throws is given by a series which comprises a great number of terms and factors if the number of counters of B is considerable; the search for the value of the unknown i which renders this series

would then be impossible if we did not reduce the same to a very convergent series. In applying to it the method of which we have just spoken, we find a very simple expression for the unknown from which it results that if, for example, B has a hundred counters, it is a bet of a little less than one against one that the game will end in 23780 throws, and a bet of a little more than one against one that it will end in 23781 throws.

These two examples added to those we have already given are sufficient to shows how the problems of games have contributed to the perfection of analysis.

CHAPTER VII.

CONCERNING THE UNKNOWN INEQUALITIES WHICH MAY EXIST AMONG CHANCES WHICH ARE SUPPOSED EQUAL.

INEQUALITIES of this kind have upon the results of the calculation of probabilities a sensible influence which deserves particular attention. Let us take the game of heads and tails, and let us suppose that it is equally easy to throw the one or the other side of the coin. Then the probability of throwing heads at the first throw is

and that of throwing it twice in succession is

But if there exist in the coin an inequality which causes one of the faces to appear rather than the other without knowing which side is favored by this inequality, the probability of throwing heads at the first throw will always be

; because of our ignorance of which face is favored by the inequality the probability of the simple event is increased if this inequality is favorable to it, just so much is it diminished if the inequality is contrary to it. But in this same ignorance the probability of throwing heads twice in succession is increased. Indeed this probability is that of throwing heads at the first throw multiplied by the probability that having thrown it at the first throw it will be thrown at the second; but its happening at the first throw is a reason for belief that the inequality of the coin favors it; the unknown inequality increases, then, the probability of throwing heads at the second throw; it consequently increases the product of these two probabilities. In order to submit this matter to calculus let us suppose that this inequality increases by a twentieth the probability of the simple event which it favors. If this event is heads, its probability will be

plus

or

and the probability of throwing it twice in succession will be the square of

, or

. If the favored event is tails, the probability of heads, will be

minus

, or

, and the probability of throwing it twice in succession will be

Since we have at first no reason for believing that the inequality favors one of these events rather than the other, it is clear that in order to have the probability of the compound event heads heads it is necessary to add the two preceding probabilities and take the half of their sum, which gives

for this probability, which

by

or by the square of the favor

that the inequality adds to the possibilities of the event which it favors. The probability of throwing tails tails is similarly

but the probability of throwing heads tails or tails heads is each

for the sum of these four probabilities ought to equal certainty or unity. We find thus generally that the constant and unknown causes which favor simple events which are judged equally possible always increase the probability of the repetition of the same simple event.

In an even number of throws heads and tails ought both to happen either an even number of times or odd number of times. The probability of each of these cases is

if the possibilities of the two faces are equal; but if there is between them an unknown inequality, this inequality is always favorable to the first case.

Two players whose skill is supposed to be equal play on the conditions that at each throw that one who loses gives a counter to his adversary, and that the game continues until one of the players has no more counters. The calculation of the probabilities shows us that for the equality of the play the throws of the players ought to be an inverse ratio to their counters. But if there is between the players a small unknown inequality, it favors that one of the players who has the smallest number of counters. His probability of winning the game increases if the players agree to double or triple their counters; and it will be

or the same as the probability of the other player in the case where the number of their counters should become infinite, preserving always the same ratio.

One may correct the influence of these unknown inequalities by submitting them themselves to the chances of hazard. Thus at the play of heads and tails, if one has a second coin which is thrown each time with the first and one agrees to name constantly heads the face turned up by the second coin, the probability of throwing heads twice in succession with the first coin will approach much nearer

than in the case of a single coin. In this last case the difference is the square of the small increment of possibility that the unknown inequality gives to the face of the first coin which it favors; in the other case this difference is the quadruple product of this square by the corresponding square relative to the second coin.

Let there be thrown into an urn a hundred numbers from I to 100 in the order of numeration, and after having shaken the urn in order to mix the numbers one is drawn; it is clear that if the mixing has been well done the probabilities of the drawing of the numbers will be the same. But if we fear that there is among them small differences dependent upon the order according to which the numbers have been thrown into the urn, we shall diminish considerably these differences by throwing into a second urn the numbers according to the order of their drawing from the first urn, and by shaking then this second urn in order to mix the numbers. A third urn, a fourth urn, etc., would diminish more and more these differences already inappreciable in the second urn.

CHAPTER VIII.

CONCERNING THE LAWS OF PROBABILITY WHICH RESULT FROM THE INDEFINITE MULTIPLICA TION OF EVENTS.

AMID the variable and unknown causes which we comprehend under the name of chance, and which render uncertain and irregular the march of events, we see appearing, in the measure that they multiply, a striking regularity which seems to hold to a design and which has been considered as a proof of Providence. But in reflecting upon this we soon recognize that this regularity is only the development of the respective possibilities of simple events which ought to present themselves more often when they are more probable. Let us imagine, for example, an urn which contains white balls and black balls; and let us suppose that each time a ball is drawn it is put back into the urn before proceeding to a new draw. The ratio of the number of the white balls drawn to the number of black balls drawn will be most often very irregular in the first drawings; but the variable causes of this irregularity produce effects alternately favorable and unfavorable to the regular march of events which destroy each other mutually in the totality of a great number of draws, allowing us to perceive more and more the ratio of white balls to the black balls contained in the urn, or the respective possibilities of drawing a white ball or black ball at each draw. From this results the following theorem.

The probability that the ratio of the number of white balls drawn to the total number of balls drawn does not deviate beyond a given interval from the ratio of the number of white balls to the total number of balls contained in the urn, approaches indefinitely to certainty by the indefinite multiplication of events, however small this interval.

This theorem indicated by common sense was difficult to demonstrate by analysis. Accordingly the illustrious geometrician Jacques Bernouilli, who first has occupied himself with it, attaches great importance to the demonstrations he has given. The calculus of discriminant functions applied to this matter not only demonstrates with facility this theorem, but still more it gives the probability that the ratio of the events observed deviates only in certain limits from the true ratio of their respective possibilities.

One may draw from the preceding theorem this consequence which ought to be regarded as a general law, namely, that the ratios of the acts of nature are very nearly constant when these acts are considered in great number. Thus in spite of the variety of years the sum of the productions during a considerable number of years is sensibly the same; so that man by useful foresight is able to provide against the irregularity of the seasons by spreading out equally over all the seasons the goods which nature distributes in an unequal manner. I do not except from the above law results due to moral causes. The ratio of annual births to the population, and that of marriages to births, show only small variations; at Paris the number of annual births is almost the same, and I have heard it said at the post-office in ordinary seasons the number of letters thrown aside on account of defective addresses changes little each year; this has likewise been observed at London.

It follows again from this theorem that in a series of events indefinitely prolonged the action of regular and constant causes ought to prevail in the long run over that of irregular causes. It is this which renders the gains of the lotteries just as certain as the products of agriculture; the chances which they reserve assure them a benefit in the totality of a great number of throws. Thus favorable and numerous chances being constantly attached to the observation of the eternal principles of reason, of justice, and of humanity which establish and maintain societies, there is a great advantage in conforming to these principles and of grave inconvenience in departing from them. If one consult histories and his own experience, one will see all the facts come to the aid of this result of calculus. Consider the happy effects of institutions founded upon reason and the natural rights of man among the peoples who have known how to establish and preserve them. Consider again the advantages which good faith has procured for the governments who have made it the basis of their conduct and how they have been indemnified for the sacrifices which a scrupulous exactitude in keeping their engagements has cost them. What immense credit at home! What preponderance abroad! On the contrary, look into what an abyss of misfortunes nations have often been precipitated by the ambition and the perfidy of their chiefs. Every time that a great power intoxicated by the love of conquest aspires to universal domination the sentiment of independence produces among the menaced nations a coalition of which it becomes almost always the victim. Similarly in the midst of the variable causes which extend or restrain the divers states, the natural limits acting as constant causes ought to end by prevailing. It is important then to the stability as well as to the happiness of empires not to extend them beyond those limits into which they are led again without cessation by the action of the causes; just as the waters of the seas raised by violent tempests fall again into their basins by the force of gravity. It is again a result of the calculus of probabilities confirmed by numerous and melancholy experiences. History treated from the point of view of the influence of constant causes would unite to the interest of curiosity that of offering to man most useful lessons. Sometimes we attribute the inevitable results of these causes to the accidental circumstances which have produced their action. It is, for example, against the nature of things that one people should ever be governed by another when a vast sea or a great distance separates them. It may be affirmed that in the long run this const...

Table of contents

• Title Page
• Copyright Page
• INTRODUCTORY NOTE
• Table of Contents
• A PHILOSOPHICAL ESSAY ON PROBABILITIES.
• PART II. - APPLICATIONS OF THE CALCULUS OF PROBABILITIES.