A Long Way from Euclid

Constance Reid

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486436135
• eBook ISBN: 9780486152028
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

Mathematics has come a long way indeed in the last 2,000 years, and this guide to modern mathematics traces the fascinating path from Euclid's Elements to contemporary concepts. No background beyond elementary algebra and plane geometry is necessary to understand and appreciate author Constance Reid's simple, direct explanations of the arithmetic of the infinite, the paradoxes of point sets, the "knotty" problems of topology, and "truth tables" of symbolic logic. Reid illustrates the ways in which the quandaries that arose from unsolvable problems promoted new ideas. Numerical concepts expanded to accommodate such concepts as zero, irrational numbers, negative numbers, imaginary numbers, and infinite numbers.
Geometry advanced into the widening territories of projective geometry, non-Euclidean geometries, the geometry of n-dimensions, and topology or "rubber sheet" geometry. More than 80 drawings, integrated with the text, assist in cultivating a grasp of the abstract foundations of modern mathematics, the search for truly consistent assumptions, the recognition that absolute consistency is unattainable, and the realization that some problems can never be solved.

1

The Golden Knot in the Golden Thread

IN ANCIENT GREECE, WHERE MODERN mathematics began, there was no question among mathematicians but that the gods themselves were mathematicians too. But were the gods arithmeticians, or were they geometers?

Number ruled the Universe, according to Pythagoras in 500 B.C. Two centuries after Pythagoras, at about the same time that Euclid was compiling the Elements, Plato was asked, “What does God do?” and had to reply, “God eternally geometrizes.” The choice of God as geometrician rather than arithmetician had quite literally been forced upon Plato and the other Greeks by two of the profoundest achievements of pre-Euclidean mathematics, both of them–ironically–due to Pythagoras and his followers.

These two achievements determined the decisive choice of form over number and set Western mathematics on the path it would follow for twenty centuries. The first was the discovery–and proof–that the square on the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides. The second was the discovery–and proof–that when the sides of a right triangle are equal there is no number which exactly measures the length of the hypotenuse.

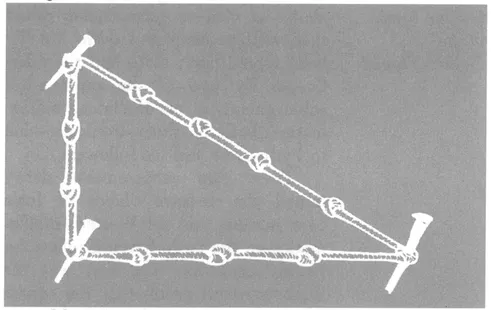
Specific instances of what we now call the Pythagorean theorem were known long before the Greeks in such far and separated parts of the world as India and China, Babylon and Egypt. In early Egypt, as the pyramids were being erected, basic right triangles were formed on the knowledge of the most familiar instance of the theorem:

3² + 4² = 5²

A rope was divided into twelve units by knots tied at equal intervals, and pegs were placed in the third, seventh, and final knots. When the rope was stretched and pegged into place, it formed of necessity the desired right triangle:

Although the Egyptians knew 3² + 4² = 5² and other similar relationships obtained by multiplying or dividing this one, we do not know if they were aware that the equation gave no mere approximation but a theoretically exact right triangle.¹

Whether this general truth was actually known earlier, history has left the discovery of the general theorem to the Greeks, and traditionally to Pythagoras. Pythagoras was in his youth a pupil of Thales, who had measured the height of the great pyramid by comparing the length of its shadow with that of a vertical stick. Later, as a teacher himself, Pythagoras opened a school of his own in his native town, where he attracted only one pupil, also named Pythagoras, whom he had to pay to keep in class. Justifiably discouraged by this lack of appreciation at home, he set out, as Thales had once advised him, for Egypt. He came at last, after years of travel and study, to southern Italy. Here he opened a school which, in contrast to his first, was one of the most wildly successful schools in history. Crowds flocked to hear Pythagoras. Besides the youths whom he instructed during the day, the business and professional leaders of the community attended his evening lectures and–to hear Pythagoras–maiden and matron alike broke the law which prohibited them from attending public meetings.²

The teachings of Pythagoras were something of a mixture–almost equal parts of morality, mysticism and mathematics. He saw life as a precarious balance of ten somewhat random but nevertheless fundamental pairs of opposites: odd and even, limited and unlimited, one and many, right and left, male and female, rest and motion, straight and curved, light and darkness, good and evil, square and oblong. It was a particularly happy circumstance for Pythagoras that the number of these fundamental opposites was 10, for from his point of view 10 was the most perfect of numbers, being the sum of 1 (the point), 2 (the line), 3 (the plane) and 4 (the solid).

Pythagoras and his followers were people who saw Number in every relationship and very personal attributes in the individual numbers.³ Their great discovery of the dependence of the musical intervals on certain arithmetic ratios of strings at the same tension provided scientific support for what they had always intuitively considered to be true:

Number rules the Universe.

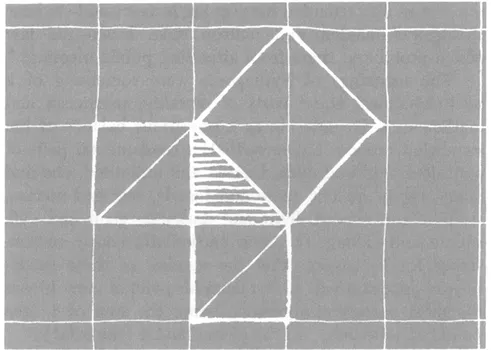
To such a people even their everyday surroundings spoke of Number. Quite probably, the first general recognition of a particular instance of the famous theorem about the square on the hypotenuse occurred when someone saw this truth as it was exhibited in the regular checkered tiling of a floor. From inspection it would have been clear that the square on the diagonal of any tile contained as many half-tiles as the squares on both sides put together:

It would also have been clear that this relationship between the diagonal (or the hypotenuse of the right angle) and the sides would remain true regardless of the size of the individual squares.

A square cut by a diagonal represents only one particular kind of right triangle–that in which the two sides containing the right angle are equal. But no one who is at all mathematically inclined, today or twenty-five hundred years ago, could observe such a truth about isosceles right triangles without wondering if it applied as well to all right triangles. Thus the general theorem would be suggested:

THEOREM: The square on the side of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides.

To make such a statement about right triangles, either we must verify it by actually examining all right triangles (which is impossible, since there are an infinite number of them) or we must prove that it is a necessary consequence of right triangle-ness and, therefore, has to be true of all right triangles.

In the centuries since the discovery of this theorem, there have been literally hundreds of proofs of the fact that the square on the hypotenuse of any right triangle is equal to the sum of the squares on the other two sides.⁴ At one time, a completely new proof was a requirement for a master’s degree in mathematics.

No one knows exactly how Pythagoras himself proved the general theorem. The proof which appeared a few hundred years later in the Elements is definitely not Pythagorean, being the only theorem in the book which tradition universally ascribes to Euclid himself.

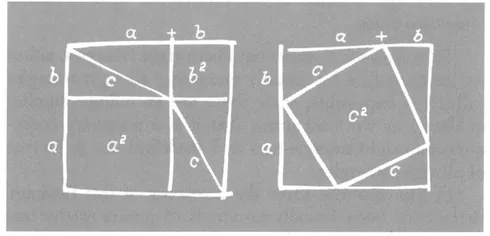
It would be pleasant to think that Pythagoras first established this great truth with one of those ingenious arrangements which bring the idea to eye and mind in the instant of seeing. Such a proof would be given by the two equal squares below with sides (a + b). These show without a word that

a² + b² = c²

since both sides of the equation, when subtracted from the two original and equal squares, leave as remainders four right triangles, all of the same size.

Although we do not know how the theorem was actually proved, tradition tells us that Pythagoras himself was so delighted (and certainly any true mathematician would have been!) that he sacrificed to the gods a hecatomb (100) of oxen, causing the theorem to be known during the Middle Ages as inventum hecatomb dignum.⁵

Thus, five hundred years before the birth of Christ, mathematics had in hand its famous theorem about the square on the hypotenuse of the right triangle–a theorem which was destined, in the words of E. T. Bell, to run “like a golden thread” through all of its history. This theorem would serve–in trigonometry, which is entirely based on it–as the tool for measurement lying beyond the immediate use of tape measure and ruler. In analytic geometry, it would serve as the basic distance formula for space in any number of dimensions. In its arithmetical generalization (aⁿ + bⁿ = cⁿ), it would provide mathematics with its most famous unsolved problem, known as Fermat’s Last Theorem.⁶ In the most revolutionary mathematical discovery of the nineteenth century, it would be revealed as the equivalent of the distinguishing axiom of Euclidean geometry; and in our own century it would be further generalized so as to be appropriate to and include geometries other than that of Euclid. Twenty-five hundred years after its first general statement and proo...

Table of contents

• Title Page
• Copyright Page
• Table of Contents
• 1 - The Golden Knot in the Golden Thread
• 2 - Nothing, Intricately Drawn Nowhere
• 3 - The Inexhaustible Storehouse
• 4 - A Number for Every Point on the Line
• 5 - Journey That Begins at O
• 6 - How Big? How Steep? How Fast?
• 7 - How Many Numbers Are Enough?
• 8 - Enchanted Realm, Where Thought Is Double
• 9 - The Possibility of Impossibility
• 10 - Euclid Not Alone
• 11 - Worlds We Make
• 12 - Where Is In and Where Is Out?
• 13 - What a Geometry IS
• 14 - Counting the Infinite
• 15 - A Most Ingenious Paradox
• 16 - The New Euclid
• 17 - Of Truth Tables and Truths
• 18 - Mathematics, the Inexhaustible
• Index