Fundamentals of the Theory of Plasticity

L. M. Kachanov

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486435831
• eBook ISBN: 9780486150826
• Topic: Technology & Engineering
• Subtopic: Civil Engineering
• Index: Technology & Engineering

Based on the author's series of lectures at the Mechanics-Mathematics Faculty of the University of Leningrad, this text is primarily concerned with the plastic deformation of metals at normal temperatures, as applied to the strength of machines and structures. Its focus on delivering a simple presentation of the basic equations of plasticity theory encompasses the best-developed methods for solving the equations; it also considers problems associated with the special nature of plastic state and the most important engineering applications of plasticity theory.
This volume traces the main trends in the theory's development, assuming readers' familiarity with the fundamentals of strength of materials and elasticity theory. Advanced topics are marked with an asterisk and can be omitted on a first reading. Intended as a text for advanced engineering students, as well as a reference book for practicing engineers, it features problems at the end of each chapter that enable readers to test their grasp of the material.
Contents include the fundamentals of continuum mechanics, equations of plastic state and elastic-plastic equilibrium, torsion, plane strain and stress, and axially symmetric strain. Additional topics range from extremum principles and energy methods of solution to theory of shakedown, stability of elastic-plastic equilibrium, dynamic problems, complex media, and viscoplasticity. An extensive bibliography appears at the end of the book. 1971 edition.

1

Basic Concepts in the Mechanics of Continuous Media

In this chapter we outline the basic formulae of the theory of stress and strain; in the process we identify the most important information for the development of the theory of plasticity.

§1. Stress

1.1. Stress

At a given point in a continuous medium the state of stress is characterized by a symmetric stress tensor

(1.1)

where σ_x, σ_y, σ_z are the normal components, and τ_xy, τ_yz, τ_xz the tangential components of stress in a rectangular coordinate system with axes x, y, z.

The stress vector p on an arbitrarily oriented surface with unit normal n (fig. 1) is given by Cauchy’s formulae:

(1.2)

where n_x, n_y, n_z are the components of the unit normal n and are equal respectively to the direction cosines cos (n, x), cos (n, y), cos (n, z).

Fig. 1.

The projection of the vector p in the direction of the normal gives the normal stress σ_n, acting on the surface in question:

(1.3)

The magnitude of the tangential stress τ_n equals

(1.4)

At each point of the medium there exist three mutually perpendicular surface elements on which the tangential stresses are zero. The directions of the normals to these surfaces constitute the principal directions of the stress tensor and do not depend on the choice of the coordinate system x, y, z. This means that any stress state at the given point may be induced by stretching the neighbourhood of the point in three mutually perpendicular directions. The corresponding stresses are called principal normal stresses; we shall denote them by σ₁, σ₂, σ₃ and number the principal axes so that

(1.5)

The stress tensor, referred to principal axes, has the form

Fig. 2.

It is not difficult to show from formulae (1.2)−(1.4) that in cross-sections, which bisect the angles between the principal planes and pass respectively through the principal axes 1, 2, 3 (fig. 2), the tangential stresses have magnitudes

The tangential stresses on these cross-sections have extremum values and are called principal tangential stresses. We define these by the formulae

(1.6)

With change in the orientation of a surface, the intensity of the tangential stress τ_n acting on it also changes. The maximum value of τ_n at a given point is called the maximum tangential stress τ_max. If condition (1.5) is satisfied, then

τ_max = −τ₂.

I...

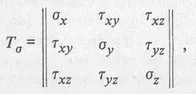
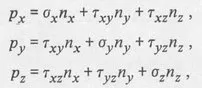
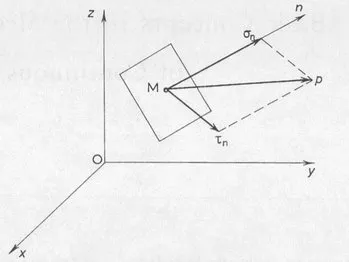
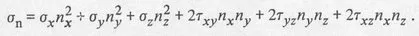
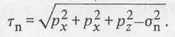
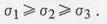
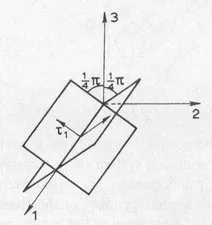
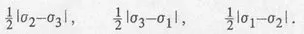
Table of contents

• DOVER BOOKS ON ENGINEERING
• Title Page
• Copyright Page
• Table of Contents
• Preface to the Second Edition
• Basic Notation
• Errata
• Introduction
• 1 - Basic Concepts in the Mechanics of Continuous Media
• 2 - Equations of the Plastic State
• 3 - Equations of Elastic-Plastic Equilibrium. The Simplest Problems
• 4 - Torsion
• 5 - Plane Strain
• 6 - Plane Stress
• 7 - Axisymmetric Strain
• 8 - Extremum Principles and Energy Methods
• 9 - Theory of Shakedown
• 10 - Stability of Elastic-Plastic Equilibrium
• 11 - Dynamical Problems
• 12 - Composite Media. Visco-Plasticity
• Appendix
• Bibliography)
• Subject Index