An Introduction to Acoustics

Robert H. Randall

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486442518
• eBook ISBN: 9780486174716
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

No branch of classical physics is older in its origins yet more modern in its applications than acoustics. Courses on acoustics very naturally begin with a study of vibrations, as a preliminary to the introduction of the wave equations. Both vibrations and waves, of course, are vastly important to all branches of physics and engineering. But it is very helpful to students to gain an understanding of mechanical waves before trying to comprehend the more subtle and abstract electromagnetic ones.
This undergraduate-level text opens with an overview of fundamental particle vibration theory, and it proceeds to examinations of waves in air and in three dimensions, interference patterns and diffraction, and acoustic impedance, as illustrated in the behavior of horns. Subsequent topics include longitudinal waves in different gases and waves in liquids and solids; stationary waves and vibrating sources, as demonstrated by musical instruments; reflection and absorption of sound waves; speech and hearing; sound measurements and experimental acoustics; reproduction of sound; and miscellaneous applied acoustics. Supplementary sections include four appendixes and answers to problems. Introduction. Appendixes. List of Symbols. References. Index. Answers to Problems.

CHAPTER 1

FUNDAMENTAL PARTICLE VIBRATION THEORY

The production of sound always involves some vibrating source. Such a source is often of irregular shape, and rarely do all parts of the vibrating surface move as a unit. It is the very complexity of the vibration of a sound source that makes it necessary to consider first the simplest vibrating body, the particle. The motion of actual sources may approximate that of a particle, particularly at low frequencies. Whenever this approximation may not be made, the vibrating surface may be broken up into smaller areas, infinitesimal if desired, the sum effect of which is equivalent to that of the total surface area of the actual source. The mathematics of this summation may be extremely complicated, but approximations will often lead to useful results.

1-1 Simple harmonic motion of a particle.

Simple harmonic motion originates, in mechanics, because of the existence of some kind of unbalanced elastic force. With such a force, Newton’s second law becomes, for a particle of mass m, free to move along the x-axis,

(1–1)

In the expression on the right for the force, K is called the elastic constant, and the negative sign indicates that the restoring force always acts towards the origin. Equation (1-1) may also be written

(1–2)

where ω² = K/m. This differential equation completely defines the type of motion and from it all other properties of simple harmonic motion may be obtained. By integrating Eq. (1-2) twice, the displacement equation may be shown to be of the form

(1–3)

where x_m. is the amplitude of the motion and α is called the phase angle. The quantities x_m and α are essentially constants of integration, whose values depend upon the mathematical boundary conditions. They may easily be determined, for instance, if one knows the value of x and of the velocity,

, at either the time t = 0, or at any other specific value of the time. Whether the cosine or the sine function appears in Eq. (1-3) is dependent upon these boundary conditions. If, for instance, α turns out to be ±π/2, Eq. (1-3) may be written in the sine form. The angular frequency, ω, is equal to 2πƒ, where f is the repetition rate in cycles per unit time.

Besides the displacement equation, two similar equations for the velocity,

, and the acceleration,

, are important:

(1–4)

(1–5)

These are obtained by a simple differentiation of Eq. (1-3). All three equations can also be obtained by considering the projection, on a diameter of a circle, of the motion of a particle moving around the circle with a constant speed, as is usually shown in elementary physics. The phase relationship is apparent from Eqs. (1–3), (1–4), and (1–5). The velocity and displacement bear a 90° relationship, while acceleration and displacement are 180° apart. The 90° relationship which always results from differentiating a sine or cosine function will be an important feature of our discussion of sound waves in air, as will be seen later.

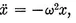
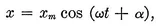
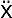
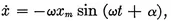
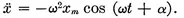
1-2 Energy in SHM.

In sound, we are always dealing with the vibration of material bodies, or media having the property of mass, and since the particle being considered is moving, it will, in general, have a kinetic energy equal to

. This energy varies with the velocity, being zero at the ends of the motion, where x = x_m, and a maximum when the particle is passing through the position x = 0. Since no dissipative force is being considered, the total energy of the system must remain constant. Therefore when the kinetic energy decreases, as the particle approaches x = x_m, the potential energy must increase. Clearly, the maximum potential energy must equal the maximum kinetic energy. The maximum potential energy,

. It is easy to show that this energy is equal to the maximum kinetic energy, (E_k)_m, possessed by the particle when it is moving through the central position. For, if

_m is the maximum velocity,

(1–6)

At positions other than the central one and the extreme end points, the energy is partly kinetic and partly potential. The total energy of the system may obviously be taken as either the maximum potential energy or the maximum kinetic energy. Using the latter,

(1–7)

It is interesting t...

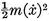
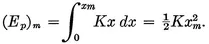
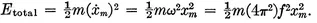
Table of contents

• Title Page
• Copyright Page
• PREFACE
• Table of Contents
• INTRODUCTION
• CHAPTER 1 - FUNDAMENTAL PARTICLE VIBRATION THEORY
• CHAPTER 2 - PLANE WAVES IN AIR
• CHAPTER 3 - WAVES IN THREE DIMENSIONS
• CHAPTER 4 - INTERFERENCE PATTERNS. DIFFRACTION
• CHAPTER 5 - ACOUSTIC IMPEDANCE. BEHAVIOR OF HORNS
• CHAPTER 6 - LONGITUDINAL WAVES IN DIFFERENT GASES. WAVES IN LIQUIDS AND SOLIDS
• CHAPTER 7 - STATIONARY WAVES. VIBRATING SOURCES. MUSICAL INSTRUMENTS
• CHAPTER 8 - REFLECTION AND ABSORPTION OF SOUND WAVES
• CHAPTER 9 - SPEECH AND HEARING
• CHAPTER 10 - SOUND MEASUREMENTS. EXPERIMENTAL ACOUSTICS
• CHAPTER 11 - REPRODUCTION OF SOUND
• CHAPTER 12 - MISCELLANEOUS APPLIED ACOUSTICS
• REFERENCES
• INDEX
• ANSWERS TO PROBLEMS