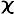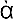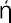A History of Mechanics

René Dugas

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486656328
• eBook ISBN: 9780486173375
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

"A remarkable work which will remain a document of the first rank for the historian of mechanics." — Louis de Broglie
In this masterful synthesis and summation of the science of mechanics, Rene Dugas, a leading scholar and educator at the famed Ecole Polytechnique in Paris, deals with the evolution of the principles of general mechanics chronologically from their earliest roots in antiquity through the Middle Ages to the revolutionary developments in relativistic mechanics, wave and quantum mechanics of the early 20th century.
The present volume is divided into five parts: The first treats of the pioneers in the study of mechanics, from its beginnings up to and including the sixteenth century; the second section discusses the formation of classical mechanics, including the tremendously creative and influential work of Galileo, Huygens and Newton. The third part is devoted to the eighteenth century, in which the organization of mechanics finds its climax in the achievements of Euler, d'Alembert and Lagrange. The fourth part is devoted to classical mechanics after Lagrange. In Part Five, the author undertakes the relativistic revolutions in quantum and wave mechanics.
Writing with great clarity and sweep of vision, M. Dugas follows closely the ideas of the great innovators and the texts of their writings. The result is an exceptionally accurate and objective account, especially thorough in its accounts of mechanics in antiquity and the Middle Ages, and the important contributions of Jordanus of Nemore, Jean Buridan, Albert of Saxony, Nicole Oresme, Leonardo da Vinci, and many other key figures.
Erudite, comprehensive, replete with penetrating insights, AHistory of Mechanics is an unusually skillful and wide-ranging study that belongs in the library of anyone interested in the history of science.

PART ONE

THE ORIGINS

CHAPTER ONE

HELLENIC SCIENCE

1. ARISTOTELIAN MECHANICS.

For lack of more ancient records, history of mechanics starts with Aristotle (384-322 B. C.) or, more accurately, with the author of the probably apocryphal treatise called Problems of Mechanics (Mηχανι

π

oβλ

ματα) . This is, in fact, a text-book of practical mechanics devoted to the study of simple machines.

In this treatise the power of the agency that sets a body in motion is defined as the product of the weight or the mass of the body—the Ancients always confused these concepts—and the velocity of the motion which the body acquires. This law makes it possible to formulate the condition of equilibrium of a straight lever with two unequal arms which carry unequal weights at their ends. Indeed, when the lever rotates the velocities of the weights will be proportional to the lengths of their supporting arms, for in these circumstances the powers of the two opposing powers cancel each other out.

The author regards the efficacy of the lever as a consequence of a magical property of the circle. “ Someone who would not be able to move a load without a lever can displace it easily when he applies a lever to the weight. Now the root cause of all such phenomena is the circle. And this is natural, for it is in no way strange that something remarkable should result from something which is more remarkable, and the most remarkable fact is the combination of opposites with each other. A circle is made up of such opposites, for to begin with it is made up of something which moves and something which remains stationary....”

In this way Problems of Mechanics. reduces the study of all simple machines to one and the same principle. “The properties of the balance are related to those of the circle and the properties of the lever to those of the balance. Ultimately most of the motions in mechanics are related to the properties of a lever. ”

To Aristotle himself, just as much in his Treatise on the Heavens, (Πε

o

ανo

) as in his Physics, concepts belonging to mechanics were not differentiated from concepts having a more general significance. Thus the notion of movement included both changes of position and changes of kind, of physical or chemical state. Aristotle’s law of powers, which he called δ

ναμις or

σχ

ς, is formulated in Chapter V of Book VII of his Physics in the following way.

“Let the motive agency be α, the moving body β, the distance travelled γ and the time taken by the displacement be δ. Then an equal power, namely the power α, will move half of β along a path twice γ in the same time, or it will move it through the distance γ in half the time δ. For in this way the proportions will be maintained. ”

Aristotle imposed a simple restriction on the application of this rule—a small power should not be able to move too heavy a body, “for then one man alone would be sufficient to set a ship in motion.”

This same law of powers reappears in Book III of the Treatise on the Heavens. Its application to statics may be regarded as the origin of the principle of virtual velocities which will be encountered much later.

In another place Aristotle made a distinction between natural motions and violent motions.

The fall of heavy bodies, for example, is a natural motion, while the motion of a projectile is a violent one.

To each thing corresponds a natural place. In this place its substantial form achieves perfection—it is disposed in such a way that it is subject as completely as possible to influences which are favourable, and so that it avoids those which are inimical. If something is moved from its natural place it tends to return there, for everything tends to perfection. If it already occupies its natural place it remains there at rest and can only be torn away by violence.

In a precise way, for Aristotle, the position of a body is the internal surface of the bodies which surround it. To his most faithful commentators, the natural place of the earth is the concave surface which defines the bottom of the sea, joined in part to the lower surface of the atmosphere, the natural place of the air.²

Concerning the natural motion of falling bodies, Aristotle maintained in Book I of the Treatise on the Heavens that the “relation which weights have to each other is reproduced inversely in their durations of fall. If a weight falls from a certain height in so much time, a weight which is twice as great will fall from the same height in half the time. ”

In his Physics (Part V), Aristotle remarked on the acceleration of falling heavy bodies. A body is attracted towards its natural place by means of its heaviness. The closer the body comes to the ground, the more that property increases.

If the natural place of heavy bodies is the centre of the World, the natural place of light bodies is the region contiguous with the Sphere of the Moon. Heavenly bodies are not subject to the laws applicable to terrestrial ones—every star is a body as it were divine, moved by its own divinity.

We return to terrestrial mechanics. All violent motion is essentially impermanent. This is one of the axioms which the Schoolmen were to repeat—Nullum violentum potest esse perpetuum. Once a projectile is thrown, the motive agency which assures the continuity of the motion resides in the air which has been set in motion. Aristotle then assumes that, in contrast to solid bodies, air spontaneously preserves the impulsion which it receives when the projectile is thrown, and that it can in consequence act as the motive agency during the projectile’s flight.

This opinion may seem all the more paradoxical in view of the fact that Aristotle remarked, elsewhere, on the resistance of the medium. This resistance increases in direct proportion to the density of the medium. “If air is twice as tenuous as water, the same moving body will spend twice as much time in travelling a certain path in water as in travelling the same path in air. ”

Aristotle also concerned himself with the composition of motions. “Let a moving body be simultaneously actuated by two motions that are such that the distances travelled in the same time are in a constant proportion. Then it will move along the diagonal of a parallelogram which has as sides two lines whose lengths are in this constant relation to each other. ” On the other hand, if the ratio between the two component distances travelled by the moving body in the same time varies from one instant to another, the body cannot have a rectilinear motion. “In such a way a curved path is generated when the moving body is animated by two motions whose proportion does not remain constant from one instant to another.”

These propositions relate to what we now call kinematics. But Aristotle immediately inferred from them dynamical results concerning the composition of forces. The connection between the two disciplines is not given, but as Duhem has indicated, it is easily supplied by making use of the law of powers—a fundamental principle of aristotelian dynamics. In particular, let us consider a heavy moving body describing some curve in a vertical plane. It is clear that the body is actuated by two motions simultaneously. Of these, one produces a vertical descent while the other, according to the position of the body on its trajectory, results in an increase or a decrease of the distance from the centre. In Aristotle’s sense, the body will have a natural falling motion due to gravity, and will be carried horizontally in a violent motion. Consider different moving bodies unequally distant from the centre of a circle and on the same radius. Let this radius, in falling, rotate about the centre. Then it may be inferred that for each body the relation of the natural to the violent motion remains the same. “The contemplation of this equality held Aristotle’s attention for a long time. He appears to have seen in it a somewhat mysterious correlation with the law of the equilibrium of levers.” ³

Aristotle believed in the impossibility of a vacuum (Physics, Book IV, Chapter XI) on the grounds that, in a vacuum, no natural motion, that is to say no tendency towards a natural place, would be possible. Incidentally this idea led him to formulate a principle analogous to that of inertia, and to justify this in the same way as that used by the great physicists of the XVIIIth Century.

“It is impossible to say why a body that has been set in motion in a vacuum should ever come to rest ; why, indeed, it should come to rest at one place rather than at another. As a consequence, it will either necessarily stay at rest or, if in motion, will move indefinitely unless some obstacle comes into collision with it. ”

Aristotle’s ideas on gravitation and the figure of the Earth merit our attention, if only because of the influence which they have had on the development of the principles of mechanics. First we shall quote from the Treatise on the Heavens (Book II, Chapter XIV). “Since the centres of the Universe and of the Earth coincide, one should ask oneself towards which of these heavy bodies and even the parts of the Earth are attracted. Are they attracted towards this point because it is the centre of the U...

Table of contents

• Title Page
• Copyright Page
• Table of Contents
• FOREWORD
• PREFACE
• PART ONE - THE ORIGINS
• PART TWO - THE FORMATION OF CLASSICAL MECHANICS
• PART THREE - THE ORGANISATION AND DEVELOPMENT OF THE PRINCIPLES OF CLASSICAL MECHANICS IN THE XVIIIth CENTURY
• PART FOUR - SOME CHARACTERISTIC FEATURES OF THE EVOLUTION OF CLASSICAL MECHANICS AFTER LAGRANGE
• PART FIVE - THE PRINCIPLES OF THE MODERN PHYSICAL THEORIES OF MECHANICS
• SOME REMARKS BY WAY OF A GENERAL CONCLUSION
• NOTES
• INDEX