Algebraic Theories

Leonard Dickson

• Publisher: Dover Publications
• Year: 2014
• ISBN:
  9780486155203
• Topic: Mathematics
• Subtopic: Algebra
• Index: Mathematics

This in-depth introduction to classical topics in higher algebra provides rigorous, detailed proofs for its explorations of some of mathematics' most significant concepts, including matrices, invariants, and groups.
Algebraic Theories studies all of the important theories; its extensive offerings range from the foundations of higher algebra and the Galois theory of algebraic equations to finite linear groups (including Klein's "icosahedron" and the theory of equations of the fifth degree) and algebraic invariants. The full treatment includes matrices, linear transformations, elementary divisors and invariant factors, and quadratic, bilinear, and Hermitian forms, both singly and in pairs. The results are classical, with due attention to issues of rationality. Elementary divisors and invariant factors receive simple, natural introductions in connection with the classical form and a rational, canonical form of linear transformations. All topics are developed with a remarkable lucidity and discussed in close connection with their most frequent mathematical applications.

CHAPTER XIII

GROUPS OF THE REGULAR SOUDS;
QUINTIC EQUATIONS

121. Introduction. The first part of this chapter gives a theory of the invariants of each finite group of linear transformations on two variables. These groups are isomorphic to groups of rotations leaving unaltered the various regular solids. The final part is an application to the resolvents of the general equation of the fifth degree and furnishes a method of solving the latter. The subject plays an important rôle in the theories of elliptic modular functions and automorphic functions.

The theory is due to Klein, whose book¹ is a classic, but presents difficulties to beginners on account of the introduction of ideas from many branches of mathematics. We shall give a simple exposition of the essentials of this interesting theory.

122. Linear fractional transformation on z corresponding to a rotation. To readers acquainted with the theory of functions of a complex variable there is available² a short proof of the desired formula (7). We shall give here a strictly elementary proof.

We first define the stereographic projection of a sphere upon a plane. Employ a rectangular coordinate system in space. The sphere with radius unity and center at the origin O has the equation

From the point N = (0, 0, 1) project an arbitrary point P = (ξ, η, ζ) of the sphere to a point Q = (x, y) of the ξη-plane.

Let T be the fourth vertex of the rectangle having sides ON and OQ. Let SPF be parallel to NO. Let FG and QH be parallel to the η-axis. Then OG = ξ, FG = η, PF = ζ, OH = x, QH = y. Since the triangles NSP and NTQ are similar,

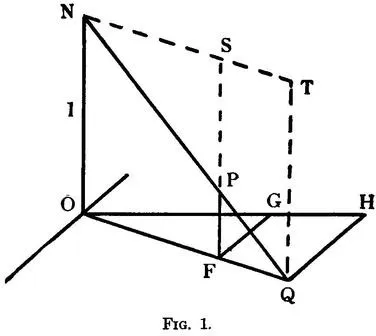
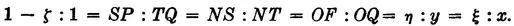
Hence

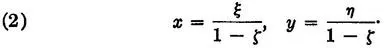
By (1),

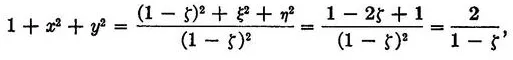
whence

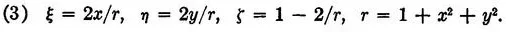
Write z = x + iy. Formulas (2) and (3) establish a one-to-one correspondence between the points of the unit sphere and the points of the complex z-plane, provided we agree to identify all points at infinity in the z-plane (so that z = ∞ alone corresponds to N).

Let E = (λ, μ, v) and P = (ξ, η, ζ) be any points on the sphere having radius unity and center at the origin O. Write

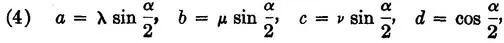
whence

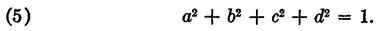
Consider the rotation about an axis OE through angle α counterclockwise when viewed from E toward O. Let it replace (ξ, η, ζ) by (ξ', η', ζ'). We employ the formulas (28) of §46 which represent the rotation, with a₁, a₂, a₃ replaced by a, b, c, and w₁, w₂, w₃ replaced by ξ, η, ζ, and p₁, p₂, p₃ replaced by ξ', η', ζ'.

Write z = x + iy, w = x − iy. Then (3) become

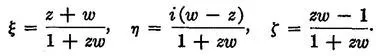
Hence

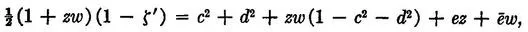
where e = bd − ac + i(ad + bc) = (b + ia) (d + ic). Replacing 1 − c² − d² by the equal value a² + b², we get

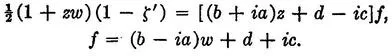
Similarly,

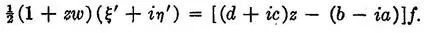
Writing z' = x' + iy', and employing (2) in accents, we get

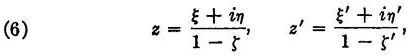
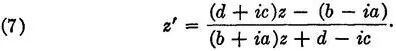
THEOREM 1. Every rotation corresponds to a transformation (7).

EXERCISES

1. By (4) and (7), with λ = μ = 0, v = 1, prove that the rotation about the ζ-axis ON through angle α counterclockwise viewed from N is represented by

2. Prove (8) by use of the formulas from analytic geometry,

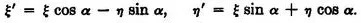
123. The tetrahedral group. Consider a cube inscribed in a sphere with the center O and radius unity. Four of its vertices 1, 2, 3, 4, shown in Fig. 2, are the vertices of a regular tetrahedron. Their diametral points 1', 2', 3', 4' are the verti...

Table of contents

• Cover
• Title
• Copyright
• Preface
• Contents
• I. Introduction to Algebraic Invariants
• II. Further Theory of Covariants of Binary Forms
• III. Matrices, Bilinear Forms, Linear Equations
• IV. Quadratic and Hermitian Forms, Symmetric and Hermitian Bilinear Forms
• V. Theory of Linear Transformations, Invariant Factors and Elementary Divisors
• VI. Pairs of Bilinear, Quadratic, and Hermitian Forms
• VII. First Principles of Groups of Substitutions
• VIII. Fields, Reducible and Irreducible Functions
• IX. Group of an Equation for a Given Field
• X. Equations Solvable by Radicals
• XI. Constructions with Ruler and Compasses
• XII. Reduction of Equations to Normal Forms
• XIII. Groups of the Regular Solids; Quintic Equations
• XIV. Representations of a Finite Group as a Linear Group; Group Characters
• Subject Index
• Author index