Interpolation

Second Edition

J. F. Steffensen

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486450094
• eBook ISBN: 9780486154831
• Edition: 2
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

In the mathematical subfield of numerical analysis, interpolation is a procedure that assists in "reading between the lines" in a set of tables by constructing new data points from existing points. This rigorous presentation employs only formulas for which it is possible to calculate error limits. Subjects include displacement symbols and differences, divided differences, formulas of interpolation, factorial coefficients, numerical differentiation, and construction of tables. Additional topics include inverse interpolation, elementary methods of summation, repeated summation, mechanical quadrature, numerical integration of differential equations, the calculus of symbols, interpolation with several variables, and mechanical cubature. 1950 edition.

§1. Introduction

1.The theory of interpolation may, with certain reservations, be said to occupy itself with that kind of information about a function which can be extracted from a table of the function. If, for certain values of the variable x₀, x₁, x₂, …, the corresponding values of the function f(x₀), f(x₁), f(x₂), … are known, we may collect our information in the table

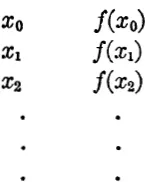
and the first question that occurs to the mind is, whether it is possible, by means of this table, to calculate, at least approximately, the value of f(x) for an argument not found in the table.

It must be admitted at once, that this problem—“interpolation” in the more restricted sense of the term—cannot be solved by means of these data alone. The table contains no other information than a correspondence between certain numbers, and if we insert another argument x and a perfectly arbitrarily chosen number f(x) as corresponding to that argument, we in no way contradict the information contained in the table.

2.It follows that, if the problem of interpolation is to have a definite, even if approximate, solution, it is absolutely indispensable to possess, beyond the data contained in the table, at least a certain general idea of the character of the function. In practice, it is a very general custom to derive formulas of interpolation on the assumption that the function with which we have to deal is a polynomial of a certain degree. The formula will, then, produce exact results if applied to a polynomial of the same or lower degree; but if it is applied to a polynomial of higher degree or to a function which is not a polynomial, nothing whatever is known about the accuracy obtained. In order to justify the application to such cases, it is customary to refer to the fact that most functions can, at least within moderate intervals, be approximated to by polynomials of a suitable degree. But this is only shirking the real difficulty; for if we have to deal with a numerical calculation, it is not sufficient to know that an approximation is obtainable; what we want to know, is how close is the approximation actually obtained.

3.A more fertile assumption, the correctness of which can often be ascertained, is that f(x) possesses, in a certain interval, a continuous differential coefficient of a certain order k. It will be shown later, that any such function can be represented as the sum of a polynomial and a “remainder-term” which is of such a simple nature, that if two numbers are known between which the differential coefficient of order k is situated, we can find limits to the error committed by neglecting the remainder-term in the interpolation.

In order to avoid having continuously to revert to the question of the assumptions made about f(x), let it be stated here once and for all, that f(x), where nothing else is expressly said, means a real, single-valued function, continuous in a closed interval, say a ≤ x ≤ b, and possessing in this interval a continuous differential coefficient of the highest order of which use is made in deriving each formula under consideration. If this order be k, f^{(k +1)} (x) need not exist at all; much less is there any necessity for assuming that f(x) is a polynomial or at least an analytical function.

Making such liberal assumptions about f(x), we will, nevertheless, be able to solve, in a simple and satisfactory manner, not only the interpolation problem in the restricted sense, but a great number of problems of a similar nature, which, taken together, form the contents of the theory of interpolation in the wider sense of the word.

4.While I assume that the reader is familiar with the notion of a “continuous function” and with the definitions of a differential coefficient and an integral, I make otherwise little use of analysis in this book. Two theorems belonging to elementary mathematical analysis are, however, so frequently referred to, that I find it practical to state them here, together with their proofs:

1.Rolle’s Theorem. If f(x) is continuous in the closed interval a ≤ x ≤ b and differentiable in the open interval a < x < b, and if f(a) = f(b) = 0, it is possible to find at least one point ξ inside the interval, such that

Proof. If f(x) is not identically zero in the interval (in which case the theorem is obvious), let m and M be the smallest and largest values it attains. As f(x) is a continuous function, at least one of these values must be attained for some argument ξ situated between a and b, as f(a) = f(b). For this value ξ we must have f′(ξ) = 0, as otherwise f(x) would be increasing or decreasing in the neighbourhood of ξ and assume values larger and smaller than f(ξ) which is impossible.

2. The Theorem of Mean Value. Let f(x) and φ(x) be integrable functions of which f(x) is continuous in the closed interval a ≤ x ≤ b, while φ(x) does not change sign in the interval. There exists, then, at least one point ξ inside the interval such that

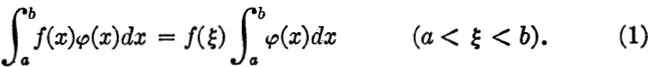
Proof. Let φ(x) be positive (otherwise we may consider − φ(x)), and let m ≤ f(x) ≤ M. Then

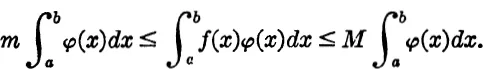
There must, therefore, exist a number μ, intermediate between m and M, such that

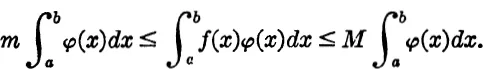
and as f(x) is continuous, μ may be replaced by f(ξ).

The Theorem of Mean Value is easily extended to double integrals and to sums; we need not go into details.

Occasionally use has been made of results, borrowed from the theory of the Gamma-Function;¹ but the student who is not familiar with that func...

Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• §1.   Introduction
• §2.   Displacement-Symbols and Differences
• §3.   Divided Differences
• §4.   Interpolation-Formulas
• §5.   Some Applications
• §6.   Factorial Coefficients
• §7.   Numerical Differentiation
• §8.   Construction of Tables
• §9.   Inverse Interpolation
• §10.  Elementary Methods of Summation
• §11.  Repeated Summation
• §12.  Laplace’s and Gauss’s Summation-Formulas
• §13.  Bernoulli’s Polynomials
• §14.  Euler’s Summation-Formula
• §15.  Lubbock’s and Wooihouse’s Formulas
• §16.  Mechanical Quadrature
• §17.  Numerical Integration of Differential Equations
• §18.  The Calculus of Symbols
• §19.  Interpolation with Several Variables
• §20.  Mechanical Cubature
• Appendix
• Index