Rockets

Two Classic Papers

Robert Goddard

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486425375
• eBook ISBN: 9780486174341
• Topic: Technology & Engineering
• Subtopic: Aeronautic & Astronautic Engineering
• Index: Technology & Engineering

Rockets, in the primitive form of fireworks, have existed since the Chinese invented them around the thirteenth century. But it was the work of American Robert Hutchings Goddard (1882-1945) and his development of liquid-fueled rockets that first produced a controlled rocket flight. Fascinated by rocketry since boyhood, Goddard designed, built, and launched the world's first liquid-fueled rocket in 1926. Ridiculed by the press for suggesting that rockets could be flown to the moon, he continued his experiments, supported partly by the Smithsonian Institution and defended by Charles Lindbergh. This book is comprised of two papers he wrote for the Smithsonian.
Among the most significant publications in the history of rockets and jet propulsion, these Smithsonian articles ― the first published in 1919 and the second in 1936 ― were issued at a time when little was known about these subjects. Goddard's first paper, "A Method of Reaching Extreme Altitudes," addressed the theoretical possibility of achieving great ranges by means of well-designed rockets. It also demonstrated that fairly high jet velocities were attainable and described advances in the construction of a solid cartridge magazine-type rocket. The second paper served as a progress report and indicated what had been accomplished through experimentation.
Goddard went to to lay the foundations for the development of long-range rockets, missiles, satellites, and spaceflight. In fact, a liquid-fueled rocket constructed on principles he developed landed humans on the moon in 1969. Today, Goddard is widely recognized as the "Father of American Rocketry." According to The New York Times, "This . . . is certainly a book that the historian of rockets cannot ignore."

A METHOD OF REACHING EXTREME ALTITUDES

By ROBERT H. GODDARD

PART I. THEORY

METHOD TO BE EMPLOYED

It is possible to obtain a suggestion as to the method that must be employed from the fundamental principles of mechanics, together with a consideration of the conditions of the problem. We are at once limited to an apparatus which reacts against matter, this matter being carried by the apparatus in question. For the entire system we must have: First, action in accordance with Newton’s Third Law of Motion; and, secondly, energy supplied from some source or sources must be used to give kinetic and potential energy to the apparatus that is being raised; kinetic energy to the matter which, by reaction, produces the desired motion of the apparatus; and also sufficient energy to overcome air resistance.

We are at once limited, since sub-atomic energy is not available, to a means of propulsion in which jets of gas are employed. This will be evident from the following consideration: First; the matter which, by its being ejected furnishes the necessary reaction, must be taken with the apparatus in reasonably small amounts. Secondly, energy must be taken with the apparatus in as large amounts as possible. Now, inasmuch as the maximum amount of energy associated with the minimum amount of matter occurs with chemical energy, both the matter and the energy for reaction must be supplied by a substance which, on burning or exploding, liberates a large amount of energy, and permits the ejection of the products that are formed. An ideal substance is evidently smokeless powder, which furnishes a large amount of energy, but does not explode with such violence as to be uncontrollable.

The apparatus must obviously be constructed on the principle of the rocket. An ordinary rocket, however, of reasonably small bulk, can rise to but a very limited altitude. This is due to the fact that the part of the rocket that furnishes the energy is but a rather small fraction of the total mass of the rocket; and also to the fact that only a part of this energy is converted into kinetic energy of the mass which is expelled. It will be expected, then, that the ordinary rocket is an inefficient heat engine. Experiments will be described below which show that this is true to a surprising degree.

By the application of several new principles, an efficiency manyfold greater than that of the ordinary rocket is possible; experimental demonstrations of which will also be described below. Inasmuch as these principles are of some value for military purposes, the writer has protected himself, as well as aerological science in America, by certain United States Letters Patent; of which the following have already been issued:

1,102,653
1,103,503
1,191,299
1,194,496.

The principles concerning efficiency are essentially three in number. The first concerns thermodynamic efficiency, and is the use of a smooth nozzle, of proper length and taper, through which the gaseous products of combustion are discharged. By this means the work of expansion of the gases is obtained as kinetic energy, and also complete combustion is ensured.

The second principle is embodied in a reloading device, whereby a large mass of explosive material is used, a little at a time, in a small, strong, combustion chamber. This enables high chamber pressures to be employed, impossible in an ordinary paper rocket, and also permits most of the mass of the rocket to consist of propellant material.

The third principle consists in the employment of a primary and secondary rocket apparatus, the secondary (a copy in minature of the primary) being fired when the primary has reached the upper limit of its flight. This is most clearly shown, in principle, in United States Patent No. 1, 102,653.

By this means the large ratio of propellant material to total mass is kept sensibly the same during the entire flight. This last principle is obviously serviceable only when the most extreme altitudes are to be reached. In order to avoid damage when the discarded casings reach the ground, each should be fitted with a parachute device, as explained in United States Patent No. 1,191,299.

Experiments will be described below which show that, by application of the above principles, it is possible to convert the rocket from a very inefficient heat engine into the most efficient heat engine that ever has been devised.

STATEMENT OF THE PROBLEM

Before describing the experiments that have been performed, it will be well to deduce the theory of rocket action in general, in order to show the tremendous importance of efficiency in the attainment of very high altitudes. A statement of the problem will therefore be made, which will lead to the differential equation of the motion. An approximate solution of this equation will be made for the initial mass required to raise a mass of one pound to any desired altitude, when said initial mass is a minimum.

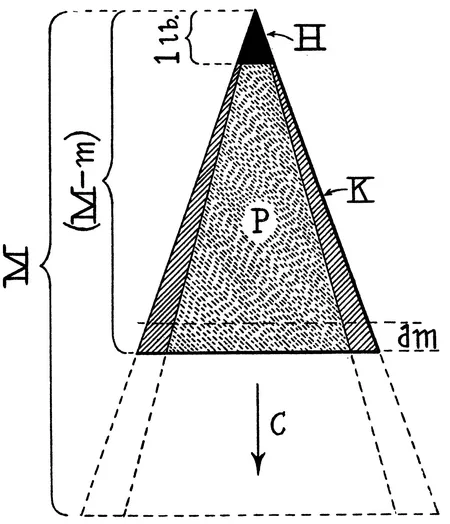
FIG. 1.

A particular form of ideal rocket is chosen for the discussion as being very amenable to theoretical treatment, and at the same time embodying all of the essential points of the practical apparatus. Referring to figure 1, a mass H, weighing one pound is to be raised as high as possible in a vertical direction ^b by a rocket formed of a cone, P, of propellant material, surrounded by a casing K. The material P is expelled downward with a constant velocity, c. It is further supposed that the casing, K, drops away continuously as the propellant material P burns, so that the base of the rocket always remains plane. It will be seen that this approximates to the case of a rocket in which the casing and firing chamber of a primary rocket are discarded after the magazine has been exhausted of cartridges, as well as to the case in which cartridge shells are ejected as fast as the cartridges are fired.

Let us call

M=the initial mass of the rocket,

m=the mass that has been ejected up to the time, t,

v=the velocity of the rocket, at time t,

c=the velocity of ejection of the mass expelled,

R=the force, in absolute units, due to air resistance,

g=the acceleration of gravity, dm=the mass expelled during the time dt,

k=the constant fraction of the mass dm that consists of casing K, expelled with zero velocity relative to the remainder of the rocket, and

dv=the increment of velocity given the remaining mass of the rocket.

The differential equation for this ideal rocket will be the analytical statement of Newton’s Third Law, obtained by equating the momentum at a time t to that at the time t+dt, plus the impulse of the forces of air resistance and gravity,

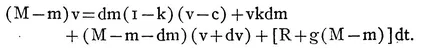
If we neglect terms of the second order, this equation reduces to

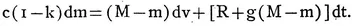
(1)

A check upon the correctness of this equation may be had from the analytical expression for the Conservation of Energy, obtained by equating the heat energy evolved by the burning of the mass of propellant, dm(1—k), to the additional kinetic energy of the system produced by this mass plus the work done against gravity and air resistance during the time dt. The equation thus derived is found to be identical with equation (1).

REDUCTION OF EQUATION TO THE SIMPLEST FORM

In the most general case, it will be found that R and g are most simply expressed when in terms of v and s. In particular, the quantity R, the air resistance of the rocket at time t, depends not only upon the density of the air and the velocity of the rocket, but also upon the cross section, S, at the time t. The cross section, S, should obviously be as small as possible; and this condition will be satisfied at all times, provided it is the following function of the mass of the rocket (M—m),

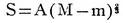
(2)

where A is a constant of proportionality. This condition is evidently satisfied by the ideal rocket, figure 1. Equation (2) expresses the fact that the shape of the rocket apparatus is at all times similar t...

Table of contents

• Title Page
• Copyright Page
• PREFACE
• Table of Contents
• FOREWORD
• A METHOD OF REACHING EXTREME ALTITUDES
• PREFACE
• A METHOD OF REACHING EXTREME ALTITUDES
• A METHOD OF REACHING EXTREME ALTITUDES
• LIQUID-PROPELLANT ROCKET DEVELOPMENT
• A Biographical Note and Appreciation