Statistical and Inductive Probabilities

Hugues Leblanc

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486449807
• eBook ISBN: 9780486154824
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

Among probability theorists, a bitter controversy has raged for decades between the adherents of John Maynard Keynes' A Treatise on Probability (1921) and those of Richard von Mises' "Grundlagen der Wahrscheinlichkeitsrechnung" (1919). Keynes declared that probabilities measure the extent to which a so-called evidence proposition supports another sentence. Von Mises insisted that they measure the relative frequency with which the members of a so-called reference set belong to another set. Statistical and Inductive Probabilities offers an evenhanded treatment of this issue, asserting that both statistical and inductive probabilities may be treated as sentence-theoretic measurements, and that the latter qualify as estimates of the former.
Beginning with a survey of the essentials of sentence theory and of set theory, author Hugues Leblanc examines statistical probabilities (which are allotted to sets by von Mises' followers), showing that statistical probabilities may be passed on to sentences, and thereby qualify as truth-values. Leblanc concludes with an exploration of inductive probabilities (which Keynes' followers allot to sentences), demonstrating their reinterpretation as estimates of truth-values.
Each chapter is preceded by a summary of its contents. Illustrations accompany most definitions and theorems, and footnotes elucidate technicalities and bibliographical references.

THE LANGUAGES L

In this first chapter I construct a family of languages, the languages L, which is to consist of a master language, called L^∞, and various fragments or sublanguages of L^∞, respectively called L¹, L², L³, and so on ad infinitum. The sets allotted probabilities in Chapter 2, for one thing, can all be mentioned in the languages L; the sentences allotted probabilities in Chapters 3 and 4, for another, will all be sentences of these languages. First, I study the vocabulary and the grammar of the languages L (Section 1–2); then, I study the interpretation to be placed upon the languages L (Section 3–4); finally, I graft onto the languages L a set theory of sorts (Section 5). The material, made up in equal parts of definitions and marginal comments thereon, should be familiar to most; it may, however, be novel to some, who will perhaps welcome a briefing on the logic of sentences and the logic of sets.¹

1. THE VOCABULARY OF THE LANGUAGES L

My first group of definitions deals with the vocabulary of the languages L. The so-called primitive signs of L^∞ are listed in D1.1; the primitive signs of the sublanguages of L^∞ are listed in D1.2; the order in which some of these signs are listed or presumed to be listed in Dl.1–2 is, for technical convenience, given a name in D1.3. Further signs, to be known as the defined signs of L^∞ and its sublanguages, will be supplied in Sections 2 and 5.

D1.1. The primitive signs of L^∞ consist of the following:

(a) The two connectives ‘~’ and ‘⊃’

(b) The quantifier letter ‘∀*;

(c) The identity sign ‘=’

(d) The comma ‘,’

(e) The two parentheses ‘(’ and ‘)’;

(f) A finite set of predicates (each identified as a one-place predicate or a two-place predicate or a three-place predicate, and so on);

(g) A denumerably infinite set of individual constants;²

(h) A denumerably infinite set of individual variables.:

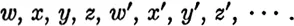
D1.2. For each N from 1 on, the primitive signs of the sublanguage L^N of L^∞ consist of the following:

(a) -(f) The various signs listed in Dl.1(a)-(D1.1(h)f);

(g) The first N individual constants listed in Dl.1(g);

(h) The individual variables listed in Dl.1(h).

D1.3. (a) The order in which the individual constants of L^∞ and its sublanguages are presumed to be listed in Dl.1(g) and Dl.2(g) is the alphabetical order of those constants.

(b) The order in which the individual variables of L^∞ and its sublanguages are listed in Dl.1(h) and Dl.2(h) is the alphabetical order of those variables³

A word of explanation on each one of clauses Dl.l (a)-(h) may be in order. The connective ~ in Dl.l (a) may be read ‘It is no...

Table of contents

• Cover
• Title Page
• Copyright page
• Dedication
• Preface
• Contents
• 1 The Languages L
• 2 Statistical Probabilities: Part One
• 3 Statistical Probabilities: Part Two
• 4 Inductive Probabilities
• List of Symbols
• Bibliographical References
• Index of Authors
• Index of Matters