Mathematical Foundations of Quantum Mechanics

George W. Mackey

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486435176
• eBook ISBN: 9780486154473
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

Designed for students familiar with abstract mathematical concepts but possessing little knowledge of physics, this text focuses on generality and careful formulation rather than problem-solving. Its author, a member of the distinguished National Academy of Science, based this graduate-level text on the course he taught at Harvard University.
Opening chapters on classical mechanics examine the laws of particle mechanics; generalized coordinates and differentiable manifolds; oscillations, waves, and Hilbert space; and statistical mechanics. A survey of quantum mechanics covers the old quantum theory; the quantum-mechanical substitute for phase space; quantum dynamics and the Schrödinger equation; the canonical "quantization" of a classical system; some elementary examples and original discoveries by Schrödinger and Heisenberg; generalized coordinates; linear systems and the quantization of the electromagnetic field; and quantum-statistical mechanics.
The final section on group theory and quantum mechanics of the atom explores basic notions in the theory of group representations; perturbations and the group theoretical classification of eigenvalues; spherical symmetry and spin; and the n-electron atom and the Pauli exclusion principle.

Chapter 1

CLASSICAL MECHANICS

1-1 Preliminaries

Let S denote the set of all “states” of a physical system, where “state” is defined in such a way that the state of the system at a time t = t₀ > 0 is uniquely determined by the appropriate physical law and the state at t = 0. For example, the state of a system of n interacting mass particles is determined by giving the 3n position coordinates and the 3n velocity coordinates of the n particles. For each s ∈ S and each t > 0 let U_t(s) denote the state at time t when the state at time 0 is s. Then for each fixed t, U_t is a transformation of S into S. Now U_t1(U_t2(s)) is the state t₁ time units after the state was U_t1(s) and U_t2(s) is the state t₂ time units after it was s. Thus U_t1(U_t2(s)) is the state t₁ + t₂ time units after it was s; that is, U_t1 + t₂(s). In other words, for all t₁ and t₂ with t₁ > 0, t₂ > 0 we have

It follows in particular that the set of all U_t is a semi-group of transformations. A semi-group which has been parameterized by the real numbers so that (1) holds is said to be a one-parameter semi-group. Thus the change in time of a physical system is described by a one-parameter semi-group. We shall call it the dynamical semi-group of the system.

If each U_t is a one-to-one map of S onto S so that

exists, we shall write

and U₀ = I, where I is the identity transformation. Then (1) holds for all real t₁ and t₂ and we have a one-parameter group. We shall deal mainly with systems that are reversible in the sense that the dynamical semi-group may be expanded to a one- parameter group as indicated above.

When our system is reversible, each s lies on one and only one “orbit,” where an orbit is the set of all points U_t(s) for fixed s and variable t. Each orbit is a curve in S. Generally speaking (we shall give precise details in various special cases) S has sufficient extra structure so that it makes sense to discuss the “tangent vectors” to the points of each orbit. In this way the dynamical group assigns a “vector” to each point of S, i. e., a “vector field.” This vector field is called the “infinitesimal generator” of the group and in many cases determines the group uniquely. This is of great importance because the physical law is usually much more easily expressed by describing the infinitesimal generator of the group than by describing the group itself. Indeed, physical laws are almost always given in infinitesimal form, and in order to obtain the orbits of the group one has to integrate differential equations.

In the special case in which S is an open subset of Euclidean n-space we may make the above considerations much more definite. (We shall consider more general cases later.) Then each orbit in S is a curve in n-space described by n functions of t: q₁(t), … , q_n(t). Here q₁(t), … , q_n(t) = U_t(q₁(0), … ,q_n(0)). If th...

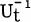
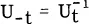
Table of contents

• Cover
• Title Page
• Copyright Page
• Editor’s Foreword
• Preface
• Contents
• Chapter 1. Classical Mechanics
• Chapter 2. Quantum Mechanics
• Chapter 3. Group Theory and the Quantum Mechanics of the Atom
• Appendix