Mathematics for the Physical Sciences

Herbert S Wilf

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486450384
• eBook ISBN: 9780486153346
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This book offers advanced undergraduates and graduate students in physics, engineering, and other natural sciences a solid foundation in several fields of mathematics. Clear and well-written, it assumes a previous knowledge of the theory of functions of real and complex variables, and is ideal for classroom use, self-study, or as a supplementary text.
Starting with vector spaces and matrices, the text proceeds to orthogonal functions; the roots of polynomial equations; asymptotic expansions; ordinary differential equations; conformal mapping; and extremum problems. Each chapter goes straight to the heart of the matter, developing subjects just far enough so that students can easily make the appropriate applications. Exercises at the end of each chapter, along with solutions at the back of the book, afford further opportunities for reinforcement. Discussions of numerical methods are oriented toward computer use, and they bridge the gap between the "there exists" perspective of pure mathematicians and the "find it to three decimal places" mentality of engineers. Each chapter features a separate bibliography.

chapter 1

Vector spaces and matrices

1.1 VECTOR SPACES

A vector space V is a collection of objects x, y, ... called vectors, satisfying the following postulates:

(I) If x and y are vectors, there is a unique vector x + y in V called the sum of x and y.

(II) If x is a vector and α a complex number, there is a uniquely defined vector αx in V satisfying

(1)

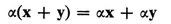
(2)

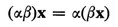
(3)

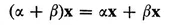
(4)

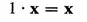
(5)

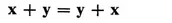
(6)

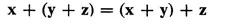
(III) There is a vector 0 in V satisfying

(7)

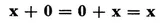
for every x in V, and, further, for every x in V there is a vector −x such that

(8)

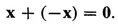
We will use the notation x − y to mean x + (− y), as might be expected.

(IV) If x and y are vectors in V, there is a uniquely defined complex number (x, y) called the “inner product” of x and y which satisfies

(9)

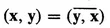
(10)

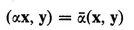
(11)

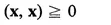
(12)

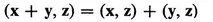
(13)

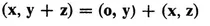
(14)

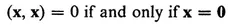
We state at once that it is not our intention to develop here a purely axiomatic theory of vector spaces. However, in the remainder of this book we shall meet several vector spaces of different types, some of which will not “look like” vector spaces at all. It is most important to note that the only qualifications a system needs in order to be a vector space¹ are those just set forth, for only in this way can the true unity of such apparently diverse topics as finite dimensional matrices, Fourier series, orthogonal polynomials, integral equations, differential eigenvalue problems, and so on, be perceived. An enlightening exercise for the reader, for example, will be found in analyzing various results as they are proved for special systems, and asking whether or not the properties of the special system were used, or whether, as will more often happen, we have proved a general property of vector spaces.

Exampl...

Table of contents

• Title Page
• Copyright Page
• Dedication
• Preface
• Table of Contents
• chapter 1 - Vector spaces and matrices
• chapter 2 - Orthogonal functions
• chapter 3 - The roots of polynomial equations
• chapter 4 - Asymptotic expansions
• chapter 5 - Ordinary differential equations
• chapter 6 - Conformal mapping
• chapter 7 - Extremum problems
• Solutions of the exercises
• Books referred to in the text
• Original works cited in the text
• Index